【题目】在平面直角坐标系中,点A,B的坐标分别为(﹣3,0),(3,0),点P在反比例函数y=![]() 的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( )
的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( )
A.2个
B.4个
C.5个
D.6个
参考答案:
【答案】D
【解析】①当∠PAB=90°时,P点的横坐标为﹣3, 把 x=﹣3 代入 y=![]() 得y=﹣
得y=﹣![]() , 所以此时P点有1个; ②当∠APB=90°, 设P(x,
, 所以此时P点有1个; ②当∠APB=90°, 设P(x,![]() ),PA2=(x+3)2+(
),PA2=(x+3)2+(![]() )2 , PB2=(x﹣3)2+(
)2 , PB2=(x﹣3)2+(![]() )2 , AB2=(3+3)2=36,因为PA2+PB2=AB2 , 所以(x+3)2+(
)2 , AB2=(3+3)2=36,因为PA2+PB2=AB2 , 所以(x+3)2+(![]() )2+(x﹣3)2+(
)2+(x﹣3)2+(![]() )2=36,整理得x4﹣9x2+4=0,所以x2=
)2=36,整理得x4﹣9x2+4=0,所以x2=![]() ,或x2=
,或x2=![]() ,所以此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,把x=3代入y=
,所以此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,把x=3代入y=![]() 得y=
得y=![]() ,所以此时P点有1个;综上所述,满足条件的P点有6个.故答案选:D.
,所以此时P点有1个;综上所述,满足条件的P点有6个.故答案选:D.
分类讨论:①当∠PAB=90°时,则P点的横坐标为﹣3,根据反比例函数图象上点的坐标特征易得P点有1个;②当∠APB=90°,设P(x,![]() ),根据两点间的距离公式和勾股定理得(x+3)2+(
),根据两点间的距离公式和勾股定理得(x+3)2+(![]() )2+(x﹣3)2+(
)2+(x﹣3)2+(![]() )2=36,此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,此时P点有1个。
)2=36,此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,此时P点有1个。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形 OABC中,OA=3,OC=5,分别以 OA、OC所在直线为x 轴、y 轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=
 (k>0)的图象经过点D且与边BA交于点E,连接DE.
(k>0)的图象经过点D且与边BA交于点E,连接DE.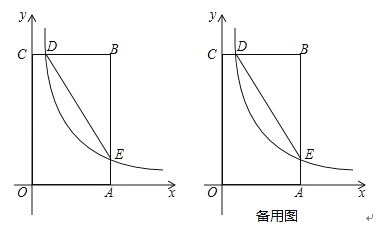
(1)连接OE,若△EOA的面积为2,则k=
(2)连接CA,DE与CA是否平行?请说明理由:
(3)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由: -
科目: 来源: 题型:
查看答案和解析>>【题目】为加强公民的节水意识,合理利用水资源.某市对居民用水实行阶梯水价,居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于1:1.5:2.如图折线表示实行阶梯水价后每月水费y(元)与用水量xm3之间的函数关系.其中线段AB表示第二级阶梯时y与x之间的函数关系。

(1)写出点B的实际意义
(2)求线段AB所在直线的表达式
(3)某户5月份按照阶梯水价应缴水费102元,其相应用水量为多少立方米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆,B为半圆上一点,连接AB并延长至C,使BC=AB,过C作CD⊥x轴于点D,交线段OB于点E,已知CD=8,抛物线经过O、E、A三点.

(1)∠OBA=
(2)求抛物线的函数表达式
(3)若P为抛物线上位于第一象限内的一个动点,以P、O、A、E为顶点的四边形面积记作S,则S取何值时,相应的点P有且只有3个? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=
 x﹣3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为
x﹣3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:cos60°﹣2﹣1+
 ﹣(π﹣3)0 .
﹣(π﹣3)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:x2+2x=3;
(2)解方程组:
相关试题

