Question

【题目】如图，在矩形 OABC中，OA=3，OC=5，分别以 OA、OC所在直线为x 轴、y 轴，建立平面直角坐标系，D是边CB上的一个动点（不与C、B重合），反比例函数y=（k＞0）的图象经过点D且与边BA交于点E，连接DE．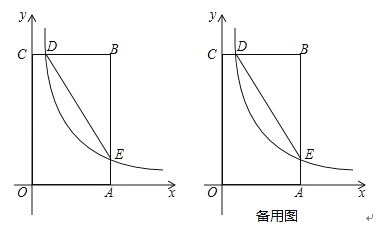

（1）连接OE，若△EOA的面积为2，则k=
（2）连接CA，DE与CA是否平行？请说明理由：
（3）是否存在点D，使得点B关于DE的对称点在OC上？若存在，求出点D的坐标；若不存在，请说明理由：

Answer 1

【答案】
（1）4
（2）

解：连接AC，如图1，

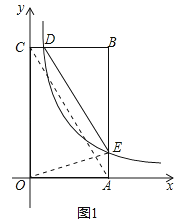
设D（x，5），E（3，），则BD=3﹣x，BE=5﹣，=,=，∴=∴DE∥AC．

（3）

解：假设存在点D满足条件．设D（x，5），E（3，），则CD=x，BD=3﹣x，BE=5﹣，AE=．作EF⊥OC，垂足为F，如图2，

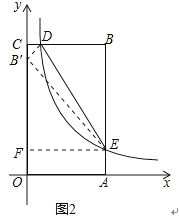
易证△B′CD∽△EFB′，∴，即=，∴B′F=，∴OB′=B′F+OF=B′F+AE=+=，

∴CB′=OC﹣OB′=5﹣，在Rt△B′CD中，CB′=5﹣，CD=x，B′D=BD=3﹣x，由勾股定理得，CB′2+CD2=B′D2，

（5﹣）2+x2=（3﹣x）2，解这个方程得，x1=1.5（舍去），x2=0.96，∴满足条件的点D存在，D的坐标为D（0.96，5）．

【解析】（1）连接OE，如，图1，∵Rt△AOE的面积为2，∴k=2×2=4．
（1）连接OE，根据反比例函数k的几何意义，即可求出k的值；（2）连接AC，设D（x，5），E（3，），则BD=3﹣x，BE=5﹣，得到=，从而求出DE∥AC．（3）假设存在点D满足条件．设D（x，5），E（3，），则CD=x，BD=3﹣x，BE=5﹣，AE=．作EF⊥OC，垂足为F，易得，△B′CD∽△EFB′，然后根据对称性求出B′E、B′D的表达式，列出 ， 即= ， ， 从而求出（5﹣）2+x2=（3﹣x）2 ， 即可求出x值，从而得到D点坐标．