【题目】如图,已知OE平分![]() ,OF平分
,OF平分![]()
![]() 若
若![]() 是直角,
是直角,![]() ,求
,求![]() 的度数.
的度数.
![]() 若
若![]() ,
,![]() ,
,![]() ,请用x的代数式来表示
,请用x的代数式来表示![]() 直接写出结果就行
直接写出结果就行![]() .
.

参考答案:
【答案】(1)45°(2)![]()
【解析】
(1)由∠AOB是直角、∠BOC=60°知∠AOC=∠AOB+∠BOC=150°,根据OE平分∠AOC、OF平分∠BOC求得∠EOC、∠COF度数,由∠EOF=∠EOC∠COF可得答案;
(2)由∠AOC=x°,、OE平分∠AOC 知∠EOC=![]() ∠AOC=
∠AOC=![]() x°,由OF平分∠BOC、∠BOC=60°知∠COF=
x°,由OF平分∠BOC、∠BOC=60°知∠COF=![]() ∠BOC=30°,根据∠EOF=∠EOC∠COF可得答案.
∠BOC=30°,根据∠EOF=∠EOC∠COF可得答案.
解:(1)∵∠AOB是直角,∠BOC=60°,
∴∠AOC=∠AOB+∠BOC=90°+60°=150°,
∵OE平分∠AOC,
∴∠EOC=![]() ∠AOC=75°,
∠AOC=75°,
∵OF平分∠BOC,
∴∠COF=![]() ∠BOC=30°,
∠BOC=30°,
∴∠EOF=∠EOC∠COF=75°30°=45°;
(2)∵∠AOC=x°,OE平分∠AOC,
∴∠EOC=![]() ∠AOC=
∠AOC=![]() x°,
x°,
∵OF平分∠BOC,∠BOC=60°,
∴∠COF=![]() ∠BOC=30°,
∠BOC=30°,
∴∠EOF=∠EOC∠COF=![]() x°30°,即y=
x°30°,即y=![]() x30.
x30.
-
科目: 来源: 题型:
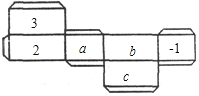
查看答案和解析>>【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空:a=______,b=______,c=______.
(2)先化简,再求值:-a2b+2(3ab2-a2b)-3(2ab2-a2b)+abc
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:[(x+y)2﹣(x﹣y)2]÷(2xy).
(2)解方程:

(3)因式分解:xy2﹣4x
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点O是正方形ABCD对角线BD的中点.
(1)如图1,若点E是OD的中点,点F是AB上一点,且使得∠CEF=90°,过点E作ME∥AD,交AB于点M,交CD于点N.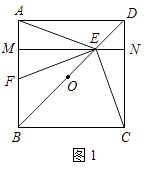
①∠AEM=∠FEM; ②点F是AB的中点;
(2)如图2,若点E是OD上一点,点F是AB上一点,且使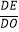 =
= 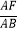 =
=  ,请判断△EFC的形状,并说明理由;
,请判断△EFC的形状,并说明理由;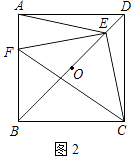
(3)如图3,若E是OD上的动点(不与O,D重合),连接CE,过E点作EF⊥CE,交AB于点F,当 =
=  时,请猜想
时,请猜想 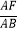 的值(请直接写出结论).
的值(请直接写出结论).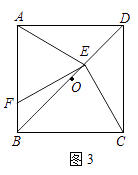
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(﹣2,﹣2)三点在格点上.

(1)作出△ABC关于y轴对称的△A1B1C1;
(2)直接写出△ABC关于x轴对称的△A2B2C2的各点坐标;
(3)求出△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC在平面直角坐标系中的位置如图所示,每个小正方形的边长为1,点A、B、C都在格点上,直线MN经过点(1,0)且垂直于
 轴,若
轴,若 和△ABC关于直线MN成轴对称.(1)请在网格中画出
和△ABC关于直线MN成轴对称.(1)请在网格中画出 ;(2)请直接写出
;(2)请直接写出 的坐标;(3)若直线上有一点P,要使△ACP的周长最小,请在图中画出点P的位置(保留画图痕迹).
的坐标;(3)若直线上有一点P,要使△ACP的周长最小,请在图中画出点P的位置(保留画图痕迹).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一副三角板按如图1方式拼接在一起,其中边OA、OC与直线EF重合,
 ,
,
 图1中
图1中 ______
______
 如图2,三角板COD固定不动,将三角板AOB绕着点O按顺时针方向旋转一个角度
如图2,三角板COD固定不动,将三角板AOB绕着点O按顺时针方向旋转一个角度 ,在转动过程中两块三角板都在直线EF的上方:
,在转动过程中两块三角板都在直线EF的上方: 当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度
当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度 的值;
的值; 是否存在
是否存在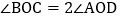 ?若存在,求此时的
?若存在,求此时的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

