搜索
【题目】（1）计算：[（x+y）2﹣（x﹣y）2]÷（2xy）．
（2）解方程：
（3）因式分解：xy2﹣4x
参考答案：
【答案】（1）2；（2）﹣28；（3）x（y+2）（y﹣2）．
【解析】
（1）根据整式的混合运算顺序和运算法则计算可得；
（2）先去分母化分式方程为整式方程，解之求得x的值，再检验即可得；
（3）先提取公因式x，再利用平方差公式分解可得．
解：（1）原式＝（x2+2xy+y2﹣x2+2xy﹣y2）÷（2xy）
＝4xy÷2xy
＝2；
（2）两边都乘以（x+4）（x﹣4），得：（x+4）2﹣6（x﹣4）＝（x+4）（x﹣4），
解得：x＝﹣28，
经检验：x＝﹣28是原分式方程的解；
（3）原式＝x（y2﹣4）＝x（y+2）（y﹣2）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】《算法统宗》是中国古代数学名著，作者是我国明代数学家程大位．在《算法统宗》中记载：“以绳测井，若将绳三折测之，绳多4尺，若将绳四折测之，绳多1尺，绳长井深各几何？”
译文：“用绳子测水井深度，如果将绳子折成三等份，井外余绳4尺；如果将绳子折成四等份，井外余绳1尺．问绳长、井深各是多少尺？”
设井深为x尺，根据题意列方程，正确的是（ ）
A. 3（x+4）=4（x+1） B. 3x+4=4x+1
C. 3（x﹣4）=4（x﹣1） D.
-
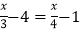
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠ACB=90°，AC=BC=4，点D为AB的中点，M，N分别在BC，AC上，且BM=CN现有以下四个结论：
①DN=DM； ② ∠NDM=90°； ③ 四边形CMDN的面积为4； ④△CMN的面积最大为2.
其中正确的结论有（ ）
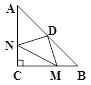
A. ①②④； B. ①②③； C. ②③④； D. ①②③④.
-
科目： 来源： 题型：
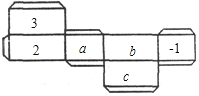
查看答案和解析>>【题目】如图是一个长方体纸盒的平面展开图，已知纸盒中相对两个面上的数互为相反数．
（1）填空：a=______，b=______，c=______．
（2）先化简，再求值：-a2b+2（3ab2-a2b）-3（2ab2-a2b）+abc
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点O是正方形ABCD对角线BD的中点．
（1）如图1，若点E是OD的中点，点F是AB上一点，且使得∠CEF=90°，过点E作ME∥AD，交AB于点M，交CD于点N．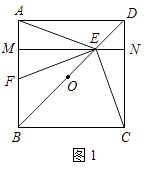
①∠AEM=∠FEM； ②点F是AB的中点；
（2）如图2，若点E是OD上一点，点F是AB上一点，且使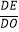
= 
= 
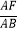，请判断△EFC的形状，并说明理由；
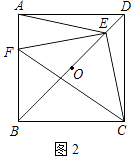
（3）如图3，若E是OD上的动点（不与O，D重合），连接CE，过E点作EF⊥CE，交AB于点F，当
= 
时，请猜想 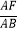的值（请直接写出结论）．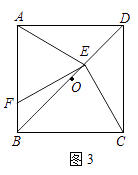
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知OE平分
，OF平分
若
是直角，
，求
的度数．
若
，
，，请用x的代数式来表示
直接写出结果就行
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示．A（2，3），B（3，1），C（﹣2，﹣2）三点在格点上．
（1）作出△ABC关于y轴对称的△A1B1C1；
（2）直接写出△ABC关于x轴对称的△A2B2C2的各点坐标；
（3）求出△ABC的面积．
相关试题
