【题目】已知一副三角板按如图1方式拼接在一起,其中边OA、OC与直线EF重合,![]() ,
,![]()
![]() 图1中
图1中![]() ______
______![]()
![]() 如图2,三角板COD固定不动,将三角板AOB绕着点O按顺时针方向旋转一个角度
如图2,三角板COD固定不动,将三角板AOB绕着点O按顺时针方向旋转一个角度![]() ,在转动过程中两块三角板都在直线EF的上方:
,在转动过程中两块三角板都在直线EF的上方:
![]() 当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度
当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度![]() 的值;
的值;
![]() 是否存在
是否存在![]() ?若存在,求此时的
?若存在,求此时的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

参考答案:
【答案】(1)75(2)①![]() ,
,![]() ,
,![]() ②当
②当![]() 或
或![]() 时,存在
时,存在![]()
【解析】
(1)根据平平角的定义即可得到结论;
(2)①根据已知条件和角平分线的定义即可得到结论;
②当OA在OD的左侧时,当OA在OD的右侧时,列方程即可得到结论.
解:(1)∵∠AOB=45°,∠COD=60°,
∴∠BOD=180°∠AOB∠COD=75°,
故答案为:75;
(2)①当OB平分∠AOD时,
∵∠AOE=α,∠COD=60°,
∴∠AOD=180°∠AOE∠COD=120°α,
∴∠AOB=![]() ∠AOD=60°
∠AOD=60°![]() α=45°,
α=45°,
∴α=30°,
当OB平分∠AOC时,
∵∠AOC=180°α,
∴∠AOB═90°![]() α=45°,
α=45°,
∴α=90°;
当OB平分∠DOC时,
∵∠DOC=60°,
∴∠BOC=30°,
∴α=180°45°30°=105°,
综上所述,旋转角度α的值为30°,90°,105°;
②当OA在OD的左侧时,则∠AOD=120°α,∠BOC=135°α,
∵∠BOC=2∠AOD,
∴135°α=2(120°α),
∴α=105°;
当OA在OD的右侧时,则∠AOD=α120°,∠BOC=135°α,
∵∠BOC=2∠AOD,
∴135°α=2(α120),
∴α=125°,
综上所述,当α=105°或125°时,存在∠BOC=2∠AOD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OE平分
 ,OF平分
,OF平分
 若
若 是直角,
是直角, ,求
,求 的度数.
的度数. 若
若 ,
, ,
, ,请用x的代数式来表示
,请用x的代数式来表示 直接写出结果就行
直接写出结果就行 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(﹣2,﹣2)三点在格点上.

(1)作出△ABC关于y轴对称的△A1B1C1;
(2)直接写出△ABC关于x轴对称的△A2B2C2的各点坐标;
(3)求出△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC在平面直角坐标系中的位置如图所示,每个小正方形的边长为1,点A、B、C都在格点上,直线MN经过点(1,0)且垂直于
 轴,若
轴,若 和△ABC关于直线MN成轴对称.(1)请在网格中画出
和△ABC关于直线MN成轴对称.(1)请在网格中画出 ;(2)请直接写出
;(2)请直接写出 的坐标;(3)若直线上有一点P,要使△ACP的周长最小,请在图中画出点P的位置(保留画图痕迹).
的坐标;(3)若直线上有一点P,要使△ACP的周长最小,请在图中画出点P的位置(保留画图痕迹).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P点作PF⊥AD交BC的延长线于点F,交AC于点H.(1)∠APB的度数为_______°;(2)求证:△ABP≌△FBP;(3)求证:AH+BD=AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一平面直角坐标系中,反比例函数y=
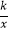 与一次函数y=kx﹣1(k为常数,且k>0)的图象可能是( )
与一次函数y=kx﹣1(k为常数,且k>0)的图象可能是( )
A.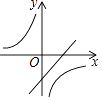
B.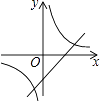
C.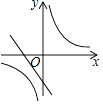
D.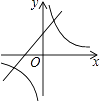
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在6×6的正方形网格中,每个小正方形的边长为1,点A、B、C、D、E、F、M、N、P均为格点(格点是指每个小正方形的顶点).
(1)利用图①中的网格,过P点画直线MN的平行线和垂线.
(2)把图②网格中的三条线段AB、CD、EF通过平移使之首尾顺次相接组成一个三角形(在图②中画出三角形).
(3)第(2)小题中线段AB、CD、EF首尾顺次相接组成一个三角形的面积是______.

相关试题

