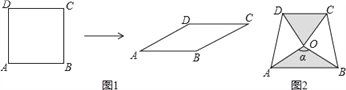
【题目】如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.
(1)请补全表:
α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
S |
| 1 |
|
(2)填空:由(1)可以发现单位正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把单位菱形的面积S记为S(α).例如:当α=30°时,S=S(30°)=![]() ;当α=135°时,S=S=
;当α=135°时,S=S=![]() .由上表可以得到S(60°)=S( °);S(30°)=S( °),…,由此可以归纳出S(α)=( °).
.由上表可以得到S(60°)=S( °);S(30°)=S( °),…,由此可以归纳出S(α)=( °).
(3)两块相同的等腰直角三角板按图2的方式放置,AD=![]() ,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
参考答案:
【答案】(1) 表中依次填写: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;(2) 120;30;α;(3) 两个带阴影的三角形面积相等,理由见解析.
;(2) 120;30;α;(3) 两个带阴影的三角形面积相等,理由见解析.
【解析】试题分析:(1)根据α,求出AB边上的高,从而用底×高得到菱形的面积;(2)在表格中找出面积相等时,角度的对应关系;(3)利用(2)中的结论求解。
试题解析:(1)当α=45°时过D作DE⊥AB于点E,
则DE=![]() AD=
AD=![]() ,∴S=ABDE=
,∴S=ABDE=![]() ,同理当α=60°时S=
,同理当α=60°时S=![]() ,
,
当α=120°时,如图2,过D作DF⊥AB,交BA的延长线于点F,
则∠DAE=60°,∴DF=![]() AD=
AD=![]() ,∴S=ABDF=
,∴S=ABDF=![]() ,
,
同理当α=150°时,可求得S=![]() ,故表中依次填写:
,故表中依次填写:![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(2)由(1)可知S(60°)=S,S=S(30°),∴S=S(α)故答案为:120;30;α;
(3)两个带阴影的三角形面积相等.
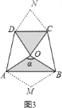
证明:如图3将△ABO沿AB翻折得到菱形AMBO,将△CDO沿CD翻折得到菱形OCND.∵∠AOD=∠COB=90°,∴∠COD+∠AOB=180°,∴S△AOB=![]() S菱形AMBO=
S菱形AMBO=![]() S(α)S△CDO=
S(α)S△CDO=![]() S
S![]() S由(2)中结论S(α)=S∴S△AOB=S△CDO.
S由(2)中结论S(α)=S∴S△AOB=S△CDO.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.

(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2
 ,CD=
,CD= BC,请求出GE的长.
BC,请求出GE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据:
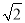 ≈1.4,
≈1.4, 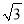 ≈1.7).
≈1.7).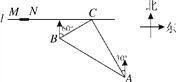
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形两边的长分别是5和9,则此三角形第三边的长可能是( )
A.1
B.4
C.8
D.14 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正多边形的内角是150°,它是_________边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面运算正确的是( )
A.7a2b﹣5a2b=2
B.x8÷x4=x2
C.(a﹣b)2=a2﹣b2
D.(2x2)3=8x6
相关试题

