搜索
【题目】如图，已知A1 ， A2 ， A3 ， …An是x轴上的点，且OA1=A1A2=A2A3=…=An﹣1An=1，分别过点A1 ， A2 ， A3 ， …An作x轴的垂线交反比例函数y= 
（x＞0）的图象于点B1 ， B2 ， B3 ， …Bn ， 过点B2作B2P1⊥A1B1于点P1 ， 过点B3作B3P2⊥A2B2于点P2…，记△B1P1B2的面积为S1 ， △B2P2B3的面积为S2…，△BnPnBn+1的面积为Sn ， 则S1+S2+S3+…+Sn= ． 
参考答案：
【答案】
【解析】解：∵OA1=A1A2=A2A3=…=An﹣1An=1，
∴设B1（1，y1），B2（2，y2），B3（3，y3），…Bn（n，yn），
∵B1 ， B2 ， B3…Bn在反比例函数y= 
（x＞0）的图象上，
∴y1=1，y2= 
，y3= 
…yn= 
，
∴S1= ×1×（y1﹣y2）= ×1×（1﹣ ）= （1﹣ ）；
S2= ×1×（y2﹣y3）= ×（ ﹣ ）；
S3= ×1×（y3﹣y4）= ×（ ﹣ 
）；
…
Sn= （ ﹣ 
），
∴S1+S2+S3+…+Sn= （1﹣ + ﹣ + ﹣ +…+ ﹣ ）= ．
所以答案是： ．
【考点精析】解答此题的关键在于理解数与式的规律的相关知识，掌握先从图形上寻找规律，然后验证规律，应用规律，即数形结合寻找规律．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，小明、小英、小丽和小华的家都在同一条街的同侧居民住宅的一排住宅楼内居住，四个家庭的住址位于同一直线上．小明家到小英家的距离约为480米，小丽家到小英家的距离约为320米，小华家在小明家和小丽家之间线段的中点的位置．
请你通过所学图形知识建立数学模型，画出图形，求出小明家和小华家的距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把△ABC纸片沿DE折叠，当点A在四边形BCDE的外部时，记∠AEB为∠1，∠ADC为∠2，则∠A、∠1与∠2的数量关系，结论正确的是（ ）
A. ∠1＝∠2＋∠A B. ∠1＝2∠A＋∠2
C. ∠1＝2∠2＋2∠A D. 2∠1＝∠2＋∠A
-
科目： 来源： 题型：
查看答案和解析>>【题目】实践探究
在数学实践课上，小明提出了这样的问题：分数
可以写为小数形式，即0.
反过来，无限循环小数0. 写成分数形式即为．那么无限循环小数0. 
应怎样化为分数呢？小明是这样思考的：
在学习解一元一次方程时，当变形到ax＝b（a≠0）形式后，通过系数化1，两边同时除以a，得到方程的解x＝
，就是分数形式．设0.
＝x，即x＝0.777…，又10x＝7.77…，这里x、0.777…、10x、7.77…存在着关系，根据这一关系我就可以找到相等关系，列出方程．请你阅读小明的思考过程，把无限循环小数0.
化为分数的过程写出来． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，转盘被等分成6个扇形，每个扇形上依次标有数字1，2，3，4，5，6．在游戏中特别规定：当指针指向边界时，重新转动转盘．
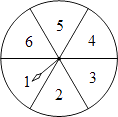
（1）自由转动转盘，当它停止转动时，指针指向的数大于4的概率为；
（2）请用画树状图法或列表法等方式求出“两次转动转盘，指针指向的数都大于4”的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（ ）
A. 4B. 3C. 2D. 1
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，A（-3，2），B（-4，-3），C（-1，-1）．
（1）在图中作出△ABC关于y轴对称的△A1B1C1；
（2）写出点△A1，B1，C1的坐标（直接写答案）：A1_________；B1________；C1________；
（3）求△A1B1C1的面积；
相关试题
