【题目】如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,求证:
(1)AC⊥BD;
(2)四边形ABCD是菱形.

参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)证得△BAC是等腰三角形后利用三线合一的性质得到AC⊥BD即可;
(2)首先证得四边形ABCD是平行四边形,然后根据对角线互相垂直得到平行四边形是菱形.
(1)∵AE∥BF,
∴∠BCA=∠CAD,
∵AC平分∠BAD,
∴∠BAC=∠CAD,
∴∠BCA=∠BAC,
∴△BAC是等腰三角形,
∵BD平分∠ABC,
∴AC⊥BD;
(2)∵△BAC是等腰三角形,
∴AB=CB,
∵∠CBD=∠ABD=∠BDA,
∴△ABD也是等腰三角形,
∴AB=AD,
∴DA=CB,
∵BC∥DA,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我县某初中为了创建书香校园,购进了一批图书.其中的20本某种科普书和30本某种文学书共花了1080元,经了解,购买的科普书的单价比文学书的单价多4元.
(1)购买的科普书和文学书的单价各多少元?
(2)另一所学校打算用800元购买这两种图书,问购进25本文学书后至多还能购进多少本科普书?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=
 CD,求证:∠AEF=90°.
CD,求证:∠AEF=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是□ABCD的边BC延长线上一点,AE交CD于点F,FG∥AD交AB于点G.
(1)填空:图中与△CEF相似的三角形有__________;(写出图中与△CEF相似的所有三角形)
(2)从(1)中选出一个三角形,并证明它与△CEF相似.

-
科目: 来源: 题型:
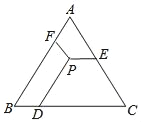
查看答案和解析>>【题目】 如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )
A. 18B. 9
C. 6D. 条件不够,不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.

(1) CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2-4x+3.
(1)在网格中,画出该函数的图象.
(2)(1)中图象与
 轴的交点记为A,B,若该图象上存在一点C,且△ABC的面积为3,求点C的坐标.
轴的交点记为A,B,若该图象上存在一点C,且△ABC的面积为3,求点C的坐标.
相关试题

