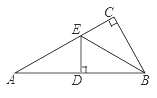
【题目】如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=6cm,
(1)求证:AE=BE ;
(2)求AB的长;
(3)若点P是AC上的一个动点,则△BDP周长的最小值=________.
参考答案:
【答案】9+3![]() .
.
【解析】(1)根据平分线的性质和三角形内角和解答即可;(2)根据勾股定理进行解答即可;(3)根据等腰三角形的性质解答即可.
解:(1)∵∠ACB=90°,∠A=30°,∠ABC=90°﹣∠A=60°
∵BE平分∠ABC,∠ABE=30°,
∴∠ABE=∠A,
∴AE=BE.
(2)∵ED⊥AB,∠A=30°,
∴ED=![]() AE=3cm.
AE=3cm.
∴![]() ,
,
∵AE=BE,DE⊥AB.
∴AB=2AD=6![]() .
.
(3)若点P是AC上的一个动点,则△BDP周长的最小值时为△BDP等腰三角形,
可得最小值为:9+3![]() .
.
故答案为:9+3![]() .
.
-
科目: 来源: 题型:
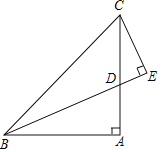
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC时
(1)若CE⊥BD于E,①∠ECD=___________0;②求证:BD=2EC;
(2)如图,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90°,点Q为∠FPC与∠PFC的角平分线的交点.当点P运动时,点Q是否一定在射线BD上?若在,请证明,若不在;请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(a-3)x+y|a|-2=1是关于x、y的二元一次方程,则a的值是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明“平行于同一条直线的两条直线互相平行”时,先假设_____成立,然后经过推理与平行公理相矛盾.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各命题都成立,而它们的逆命题不能成立的是( ).
A.两直线平行,同位角相等 B.全等三角形的对应角相等
C.四边相等的四边形是菱形 D.直角三角形中, 斜边的平方等于两直角边的平方和
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=5,C是直线AB上一点,BC=2,则线段AC长为
A. 3 B. 7 C. 3或7 D. 以上都不对
-
科目: 来源: 题型:
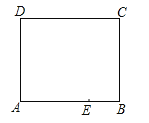
查看答案和解析>>【题目】如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是 .
相关试题

