【题目】已知关于x的一元二次方程mx2-(3m+2) x+2m+2=0(m>0).
(1)求证:方程有两个不相等的实数根且其中一个根为定值;
(2)设方程的两个实数根分别为x1、x2(其中x1<x2),若y是关于m的函数,且y=7x1-mx2,求这个函数的表达式;并求当自变量m的取值范围满足什么条件时,y≤3m.
参考答案:
【答案】(1)证明见解析;(2)y=-2m+5;当m≥1时,y≤3m.
【解析】试题分析:(1)先计算判别式的值得到△=(m+2)2,由m>0,得到△>0,根据判别式的意义得到方程有两个不相等的实数根,再利用求根公式得到x=![]() ,可得到方程有一个根为1,于是得到方程有两个不相等的实数根且其中一根为定值.
,可得到方程有一个根为1,于是得到方程有两个不相等的实数根且其中一根为定值.
(2)解方程得到x1=1,x2=2+![]() ,所以y=7-m(2+
,所以y=7-m(2+![]() )=-2m+5,然后解不等式-2m+5≤3m.
)=-2m+5,然后解不等式-2m+5≤3m.
试题解析:(1)证明:△=(3m+2)2-4m(2m+2)
=m2+4m+4
=(m+2)2,
∵m>0,
∴(m+2)2>0,即△>0,
∴方程有两个不相等的实数根,
∵x=![]() ,
,
∴方程有一个根为1,
∴方程有两个不相等的实数根且其中一根为定值.
(2)∵x=![]() ,
,
∴x1=1,x2=2+![]() ,
,
∴y=7x1-mx2
=7-m(2+![]() )
)
=-2m+5,
当y≤3m,即-2m+5≤3m,
∴m≥1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中,是准确数的是( )。
A.小明身高大约165cm
B.天安门广场约44万平方米
C.天空中有8只飞鸟
D.国庆长假到北京旅游的有60万人 -
科目: 来源: 题型:
查看答案和解析>>【题目】今年春节我市共接待国内外游客总人数3343200万人次,3343200这个数用科学记数法表示为( )
A.0.33432×106
B.3.3432×106
C.3.3432×105
D.33.432×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上,修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的甬道,设甬道的宽为a米.
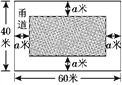 ①
①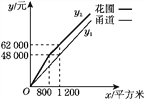 ②
②(1)用含a的式子表示花圃的面积;
(2)如果甬道所占面积是整个长方形空地面积的
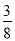 ,求此时甬道的宽;
,求此时甬道的宽;(3)已知某园林公司修建甬道、花圃的造价y1(元)、y2(元)与修建面积x(平方米)之间的函数关系如图②所示.如果学校决定由该公司承建此项目,并要求修建的甬道宽不少于2米且不超过10米,那么甬道的宽为多少米时,修建的甬道和花圃的总造价最低?最低总造价为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. (a3)2=a6B. a2·a4=a8C. a6÷a2=a3D. 3a2-a2=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式 x3+(﹣k+1)2x2﹣3x+1 中不含 x2 项,则 k 的值为( )
A. 0 B. 1 C. ﹣1 D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师布置了两道解方程的作业题:
(1)选用合适的方法解方程:(x+1)(x+2)=6;
(2)用配方法解方程:2x2+4x-5=0.
以下是小明同学的作业:
(1)解:由(x+1)(x+2)=6,
(2)解:由2x2+4x-5=0,
得x+1=2,x+2=3,
得2x2+4x=5,
所以x1=1,x2=1.
x2+2x=
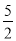 ,
,x2+2x+1=
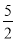 -1,
-1,(x+1)2=
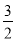 ,
,x+1=±
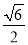
x1=-1+
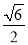 ,x2=-1-
,x2=-1-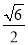 .
.请你帮小明检查他的作业是否正确,把不正确的改正过来.
相关试题

