【题目】李老师布置了两道解方程的作业题:
(1)选用合适的方法解方程:(x+1)(x+2)=6;
(2)用配方法解方程:2x2+4x-5=0.
以下是小明同学的作业:
(1)解:由(x+1)(x+2)=6, | (2)解:由2x2+4x-5=0, |
得x+1=2,x+2=3, | 得2x2+4x=5, |
所以x1=1,x2=1. | x2+2x= |
x2+2x+1= | |
(x+1)2= | |
x+1=± | |
x1=-1+ |
请你帮小明检查他的作业是否正确,把不正确的改正过来.
参考答案:
【答案】(1) x1=1,x2=-4.(2) x1=-1+![]() ,x2=-1-
,x2=-1-![]() .
.
【解析】试题分析:(1)先整理方程,然后进行因式分解,再求解即可;
(2)首先把方程的二次项系数化为1,移项,然后在方程的左右两边同时加上一次项系数一半的平方,左边就是完全平方式,右边就是常数,然后利用平方根的定义即可求解.
试题解析:(1)(x+1)(x+2)=6,
x2+3x+2-6=0,
即x2+3x-4=0,
∴(x+4)(x-1)=0,
∴x1=-4,x2=1;
(2)由原方程,得
2x2+4x=5,
x2+2x=![]() ,
,
(x+1)2=1+![]() ,即(x+1)2=
,即(x+1)2=![]() .
.
x+1=±![]()
∴x1=-1+![]() ,x2=-1-
,x2=-1-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程mx2-(3m+2) x+2m+2=0(m>0).
(1)求证:方程有两个不相等的实数根且其中一个根为定值;
(2)设方程的两个实数根分别为x1、x2(其中x1<x2),若y是关于m的函数,且y=7x1-mx2,求这个函数的表达式;并求当自变量m的取值范围满足什么条件时,y≤3m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. (a3)2=a6B. a2·a4=a8C. a6÷a2=a3D. 3a2-a2=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式 x3+(﹣k+1)2x2﹣3x+1 中不含 x2 项,则 k 的值为( )
A. 0 B. 1 C. ﹣1 D. 不确定
-
科目: 来源: 题型:
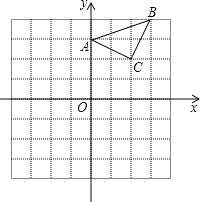
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程ax2+bx+c=0(a≠0).有下列命题:①若a+b+c=0,则b2-4ac≥0;②若一元二次方程ax2+bx+c=0的两根为-1和2,则2a+c=0;③若一元二次方程ax2+c=0有两个不相等的实数根,则一元二次方程ax2+bx+c=0必有两个不相等的实数根.其中真命题的个数是( )
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+4x+k=0有两个实数根,则k的取值范围是( )
A.k≤﹣4
B.k≥﹣4
C.k≤4
D.k>4
相关试题

