【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
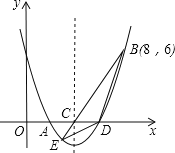
(1)求二次函数的解析式.
(2)求函数图象的顶点坐标及D点的坐标.
(3)该二次函数的对称轴交x轴于C点,连接BC,并延长BC交抛物线于E点,连接BD,DE,直接写出△BDE的面积.
参考答案:
【答案】(1)y=![]() x2﹣4x+6;(2)顶点坐标为(4,﹣2),y=
x2﹣4x+6;(2)顶点坐标为(4,﹣2),y=![]() x2﹣4x+6;(3)
x2﹣4x+6;(3)![]() .
.
【解析】
试题分析:(1)把A(2,0),B(8,6)代入y=![]() x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
(2)先把(1)中的解析式配成顶点式即可得到顶点坐标,然后利用抛物线对称性确定D点坐标;
(3)先利用待定系数法求出直线BC的解析式,再利用解方程组 得E点坐标,然后利用S△BDE=S△BDC+S△EDC进行计算即可.
得E点坐标,然后利用S△BDE=S△BDC+S△EDC进行计算即可.
解:(1)把A(2,0),B(8,6)代入y=![]() x2+bx+c得
x2+bx+c得 ,解得
,解得![]() ,
,
所以二次函数解析式为y=![]() x2﹣4x+6;
x2﹣4x+6;
(2)y=![]() x2﹣4x+6=
x2﹣4x+6=![]() (x﹣4)2﹣2,
(x﹣4)2﹣2,
所以二次函数图象的顶点坐标为(4,﹣2),
由于抛物线的对称轴为直线x=4,而A(2,0),
所以D点坐标为(6,0);
(3)C(4,0),
设直线BC的解析式为y=mx+n,
把B(8,6),C(4,0)代入得![]() ,解得
,解得 ,
,
所以直线BC的解析式为y=![]() x﹣6,
x﹣6,
解方程组 得
得 或
或![]() ,
,
所以E点坐标为(3,﹣![]() ),
),
所以S△BDE=S△BDC+S△EDC=![]() ×(6﹣4)×6+
×(6﹣4)×6+![]() ×(6﹣4)×
×(6﹣4)×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将纸片△ABC沿DE折叠使点A落在A′处的位置.
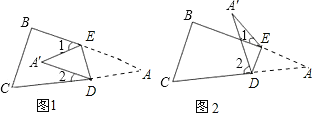
(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.
(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是 .
(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:∠C=90°,∠DBC=30°,AB=BD,利用此图可求得tan75°的值是( )

A.2﹣
 B.2+
B.2+ C.
C. ﹣2 D.
﹣2 D. +1
+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象如图所示,则ax2+bx+c+m=0的实数根的条件是( )
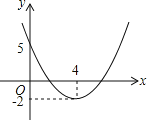
A.m≥﹣2 B.m≤﹣2 C.m≤2 D.m≥2
-
科目: 来源: 题型:
查看答案和解析>>【题目】 小明同学5次数学单元测试的平均成绩是90分,中位数是91分,众数是94分,则两次最低成绩之和是( )
A. 165分 B. 168分 C. 170分 D. 171分
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:-x·(-x2)·(-x)3=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列能平方差公式计算的式子是( )
A. (a﹣b)(b﹣a) B. (﹣x+1)(x﹣1)
C. (﹣a﹣1)(a+1) D. (﹣x﹣y)(﹣x+y)
相关试题

