【题目】将纸片△ABC沿DE折叠使点A落在A′处的位置.
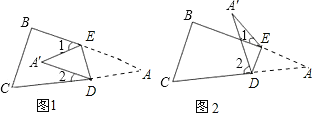
(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.
(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是 .
(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.
参考答案:
【答案】(1)2∠A=∠1+∠2,理由见解析;(2)2∠A=∠2;(3)2∠A=∠2﹣∠1,理由见解析.
【解析】
试题分析:(1)根据折叠性质得出∠AED=∠A′ED,∠ADE=∠A′DE,根据三角形内角和定理得出∠AED+∠ADE=180°﹣∠A,代入∠1+∠2=180°+180°﹣2(∠AED+∠ADE)求出即可;
(2)根据三角形外角性质得出∠DME=∠A′+∠1,∠2=∠A+∠DME,代入即可求出答案.
解:(1)图1中,2∠A=∠1+∠2,
理由是:∵延DE折叠A和A′重合,
∴∠AED=∠A′ED,∠ADE=∠A′DE,
∵∠AED+∠ADE=180°﹣∠A,∠1+∠2=180°+180°﹣2(∠AED+∠ADE),
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A;
(2)2∠A=∠2,如图

∠2=∠A+∠EA′D=2∠A,
故答案为:2∠A=∠2;
(3)如图2,2∠A=∠2﹣∠1,
理由是:∵延DE折叠A和A′重合,

∴∠A=∠A′,
∵∠DME=∠A′+∠1,∠2=∠A+∠DME,
∴∠2=∠A+∠A′+∠1,
即2∠A=∠2﹣∠1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个正方形在四月份的日历上圈出4个数,这四个数字的和不可能是( )
A. 104 B. 24 C. 108 D. 28
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意有理数a,b,现用“☆”定义一种运算:a☆b=a2﹣b2,根据这个定义,代数式(x+y)☆y可以化简为( )
A. xy+y2 B. xy﹣y2 C. x2+2xy D. x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.
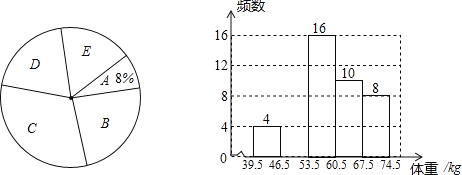
解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:∠C=90°,∠DBC=30°,AB=BD,利用此图可求得tan75°的值是( )

A.2﹣
 B.2+
B.2+ C.
C. ﹣2 D.
﹣2 D. +1
+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象如图所示,则ax2+bx+c+m=0的实数根的条件是( )
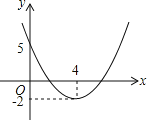
A.m≥﹣2 B.m≤﹣2 C.m≤2 D.m≥2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=
 x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).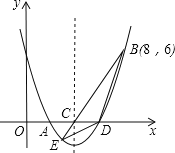
(1)求二次函数的解析式.
(2)求函数图象的顶点坐标及D点的坐标.
(3)该二次函数的对称轴交x轴于C点,连接BC,并延长BC交抛物线于E点,连接BD,DE,直接写出△BDE的面积.
相关试题

