Question

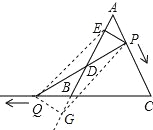
【题目】如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动（与A、C不重合），Q是CB延长线上一动点，与点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，PF∥BC交AB于F，连接PQ交AB于D．

（1）当∠BQD=30°时，求AP的长；

（2）当运动过程中线段ED的长始终保持不变，试求出ED的长度．

Answer 1

【答案】（1）2；（2）3．

【解析】

试题分析：（1）由△ABC是边长为6的等边三角形，可知∠ACB=60°，再由∠BQD=30°可知∠QPC=90°，设AP=x，则PC=6﹣x，QB=x，在Rt△QCP中，∠BQD=30°，PC=QC，即6﹣x=（6+x），求出x的值即可；

（2）作QG⊥AB，交直线AB于点G，连接QE，PG，由点P、Q做匀速运动且速度相同，可知AP=BQ，再根据全等三角形的判定定理得出△APE≌△BQG，再由AE=BG，PE=QG且PE∥QG，可知四边形PEQG是平行四边形，进而可得出EB+AE=BE+BG=AB，DE=AB，由等边△ABC的边长为6，可得出DE=3．

试题解析：（1）∵△ABC是边长为6的等边三角形，∴∠ACB=60°，∵∠BQD=30°，∴∠QPC=90°，设AP=x，则PC=6﹣x，QB=x，∴QC=QB+BC=6+x，∵在Rt△QCP中，∠BQD=30°，∴PC=QC，即6﹣x=（6+x），解得x=2，∴AP=2；（2）作QG⊥AB，交直线AB于点G，连接QE，PG，又∵PE⊥AB于E，∴∠DGQ=∠AEP=90°，∵点P、Q速度相同，∴AP=BQ，∵△ABC是等边三角形，∴∠A=∠ABC=∠GBQ=60°，在△APE和△BQG中，∵∠AEP=∠BGQ=90°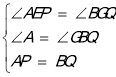，，∴△APE≌△BQG（AAS），∴AE=BG，PE=QG且PE∥QG，∴四边形PEQG是平行四边形，∴DE=EG，∵EB+AE=BE+BG=AB=EG，∴DE=AB，又∵等边△ABC的边长为6，∴DE=3，故运动过程中线段ED的长始终为3．