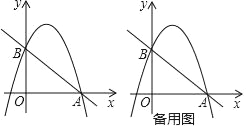
【题目】已知:如图,抛物线y=﹣x2+bx+C经过点B(0,3)和点A(3,0)
(1)求该抛物线的函数表达式和直线AB的函数表达式;
(2)若直线l⊥x轴,在第一象限内与抛物线交于点M,与直线AB交于点N,请在备用图上画出符合题意的图形,并求点M与点N之间的距离的最大值或最小值,以及此时点M,N的坐标.
参考答案:
【答案】(1) 抛物线的函数表达式是y=﹣x2+2x+3;直线AB的函数表达式是y=﹣x+3;(2) 点M与点N之间的距离有最大值![]() ;点M坐标为(
;点M坐标为(![]() ,
,![]() )点N的坐标为(
)点N的坐标为(![]() ,
,![]() ).
).
【解析】整体分析:
(1)把点B(0,3)和点A(3,0)代入到y=-x2+bx+c和一次函数的一般式中求解;(2)设直线l的横坐标为a,分别用a表示出点M,N的坐标,然后用a表示出MN的长,用配方法即可求出MN的最大值.
解:(1)∵抛物线y=-x2+bx+c经过点B(0,3)和点A(3,0),
![]() 解得
解得![]()
抛物线的函数表达式是y=-x2+2x+3;
设直线AB:y=kx+m,根据题意得![]() ,解得
,解得![]() ,
,
直线AB的函数表达式是y=-x+3;
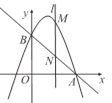
(2)如图,设直线l的横坐标为a,
则点M的坐标为(a,-a2+2a+3),点N的坐标是(a,-a+3),
又点M,N在第一象限,
∴|MN|=-a2+2a+3-(-a+3)=-a2+3a,
又|MN|=-a2+3a=-(a2-3a+![]() )+
)+![]() =
=![]() ,
,
当a=![]() 时,|MN|有最大值,最大值为
时,|MN|有最大值,最大值为![]() ,
,
即点M与点N之间的距离有最大值![]() ,
,
此时点M坐标为(![]() ,
,![]() ),点N的坐标为
),点N的坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法,……,据此解答下面的问题
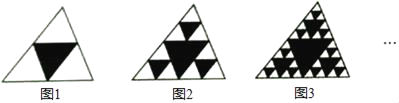
(1)填写下表:
图形
挖去三角形的个数
图形1
1
图形2
1+3
图形3
1+3+9
图形4
(2)根据这个规律,求图n中挖去三角形的个数wn;(用含n的代数式表示)
(3)若图n+1中挖去三角形的个数为wn+1,求wn+1﹣Wn
-
科目: 来源: 题型:
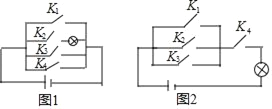
查看答案和解析>>【题目】小明学习电学知识后,用四个开关按键(每个开关键闭合的可能性相等)、一个电源和一个灯泡设计了一个电路图
(1)若小明设计的电路图(四个开关按键都处于打开状态)如图所示,求任意闭合一个开关按键,灯泡能发光的概率;
(2)若小明设计的电路图(四个开关按键都处于打开状态)如图所示,求同时闭合其中的两个开关按键,灯泡能发光的概率.(用列表或树状图法)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c三个数在数轴上对应点的位置如图所示,下列几个判断:①a<c<b;②ab<0;③a+b>0;④c﹣a<0中,错误的有( )个.
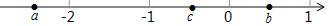
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】用无刻度的直尺按要求作图,请保留画图痕迹,不需要写作法.
(1)如图1,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是矩形.请你只用无刻度的直尺在图中画出∠AOB的平分线.
(2)如图2,在8×6的正方形网格中,请用无刻度直尺画一个与△ABC面积相等,且以BC为边的平行四边形,顶点在格点上.

-
科目: 来源: 题型:
查看答案和解析>>【题目】绿水青山就是金山银山,国家倡导全民植树。在今年3月12日植树节当天,某校七年级一班48名学生全部参加了植树活动,男生每人栽种4株,女生每人栽种3株,全班共栽种170株。
(1)该班男、女生各为多少人?
(2)学校选择购买甲、乙两种树苗,甲树苗
 ,乙树苗
,乙树苗 .如果要使购买树苗的钱不超过1200元,那么最多可以购买甲树苗多少株?
.如果要使购买树苗的钱不超过1200元,那么最多可以购买甲树苗多少株? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米?

相关试题

