【题目】如图,已知⊙O的弦AB等于半径,连接OB并延长使BC=OB.
(1)∠ABC= .
(2)AC与⊙O有什么关系?请证明你的结论;
(3)在⊙O上,是否存在点D,使得AD=AC?若存在,请画出图形,并给出证明;若不存在,请说明理由.

参考答案:
【答案】(1)120°;(2)AC是⊙O的切线,证明见解析;(3)存在.证明见解析.
【解析】解:(1)120°;……………………………………………………………1分
(2)AC是⊙O的切线.……………………………………………………3分
证法一
∵AB=OB=OA,∴△OAB为等边三角形,…………………………4分
∴∠OBA=∠AOB=60°.……………………………………………5分
∵BC=BO,∴BC=BA,
∴∠C=∠CAB,……………………………………………………………6分
又∵∠OBA=∠C+∠CAB=2∠C,
即2∠C=60°,∴∠C=30°,………………………………………7分
在△OAC中,∵∠O+∠C=60°+30°=90°,
∴∠OAC=90°,…………………………………………………………8分
∴AC是⊙O的切线;
证法二:
∵BC=OB,∴点B为边OC的中点,……………………………………4分
即AB为△OAC的中位线,…………………………………………………5分
∵AB=OB=BC,即AB是边OC的一半,……………………………6分
∴△OAC是以OC为斜边的直角三角形,…………………………………7分
∴∠OAC=90°,…………………………………………………………8分
∴AC是⊙O的切线;
(3)存在.……………………………………………………………………9分
方法一:
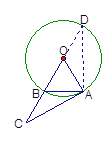
如图2,延长BO交⊙O于点D,即为所求的点.…………………………10分
证明如下:
连结AD,∵BD为直径,∴∠DAB=90°.…………………………11分
在△CAO和△DAB中,
∵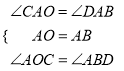 ,∴△CAO≌△DAB(ASA),………………12分
,∴△CAO≌△DAB(ASA),………………12分
∴AC=AD.…………………………………………………………………13分
(也可由OC=BD,根据AAS证明;或HL证得,或证△ABC≌△AOD)
方法二:
如图3,画∠AOD=120°,……………………………………………10分
OD交⊙O于点D,即为所求的点.…………………………………………11分
∵∠OBA=60°,
∴∠ABC=180°-60°=120°.
在△AOD和△ABC中,
∵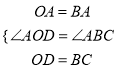 ,∴△AOD≌△ABC(SAS),………………12分
,∴△AOD≌△ABC(SAS),………………12分
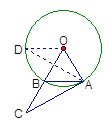
∴AD=AC.…………………………………………………………………13分
(1)由已知可知△AOB为等边三角形,利用平角求出∠ABC的度数
(2)利用直角三角形的性质求出∠OAC=90°,从而得出结论
(3)延长BO交⊙O于点D,即为所求的点,利用全等三角形求证
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△OAB的顶角∠AOB=30°,点B在x轴上,腰OA=4
(1)B点得坐标为: ;
(2)画出△OAB关于y轴对称的图形△OA1B1(不写画法,保留画图痕迹),求出A1与B1的坐标;
(3)求出经过A1点的反比例函数解析式.(注:若涉及无理数,请用根号表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知P是直线l外一点, A、B、C是直线l上一点,且PA=5,PB=3,PC=2,那么点P到直线l的距离为( ).
A. 等于2 B. .大于2C. 小于或等于2D. 小于2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2+kx+2k﹣4
(1)当k=2时,求出此抛物线的顶点坐标;
(2)求证:无论k为任何实数,抛物线都与x轴有交点,且经过x轴一定点;
(3)已知抛物线与x轴交于A(x1,0)、B(x2,0)两点(A在B的左边),|x1|<|x2|,与y轴交于C点,且S△ABC=15.问:过A,B,C三点的圆与该抛物线是否有第四个交点?试说明理由.如果有,求出其坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列下列命题是真命题的是( )
A. 过一点有且只有一条直线与已知直线垂直
B. 相等的两个角一定是对顶角
C. 将一根细木条固定在墙上,只需要一根钉子
D. 同角的余角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,E、F分别为矩形ABCD的边AD和BC上的点,AE=CF.求证:BE=DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A. 平行四边形的对角线相等 B. 矩形的对角线平分对角
C. 菱形的对角线互相平分 D. 梯形的对角线互相垂直
相关试题

