【题目】如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移2格,再向上平移3格,其中每个格子的边长为1个单位长度。
(1)画出△ABC边AB上的高;
(2)请在图中画出平移后的三角形A’B’C’;
(3)若连接BB′,CC′,则这两条线段之间的关系是_____________________

参考答案:
【答案】(1)见解析;(2)见解析;(3)BB′//CC′且BB′=CC′
【解析】
(1)利用网格,过点C作出线段AB的垂线即可;
(2)根据网格结构找出对应点A′、B′、C′的位置,然后顺次连接即可;
(3)结合图形,利用平移的性质即可得出结论.
解:(1)如图所示,过点C组CH⊥AB,交AB的延长线于点H,则线段CH即为△ABC边AB上的高;
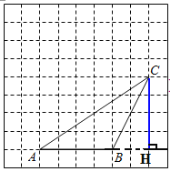
(2)△A′B′C′如图所示:
(3)如上图,连接BB′,CC′,根据平移的性质:平移前后,对应点之间的连线段互相平行(或在一条直线上)且相等,故BB′//CC′且BB′=CC′
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2x﹣m=0有两个实数根.
(1)求实数m的取值范围;
(2)若方程的两个实数根为x1、x2 , 且x1x2=2m2﹣1,求实数m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,点
,点 在点
在点 的右侧,
的右侧, ,
, 的平分线交于点
的平分线交于点 (不与
(不与 ,
, 点重合),
点重合), .设
.设 .
.
(1)若点
 在点
在点 的左侧,求
的左侧,求 的度数(用含
的度数(用含 的代数式表示)
的代数式表示)(2)将(1)中的线段
 沿
沿 方向平移,当点
方向平移,当点 移动到点
移动到点 右侧时,请画出图形并判断
右侧时,请画出图形并判断 的度数是否改变.若改变,请求出
的度数是否改变.若改变,请求出 的度数(用含
的度数(用含 的代数式表示);若不变,请说明理由.
的代数式表示);若不变,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了保护环境,某公交公司决定购买A、B两种型号的全新混合动力公交车共10辆,其中A种型号每辆价格为a万元,每年节省油量为
 万升;B种型号每辆价格为b万元,每年节省油量为
万升;B种型号每辆价格为b万元,每年节省油量为 万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元. 请求出a和b;
请求出a和b; 若购买这批混合动力公交车每年能节省
若购买这批混合动力公交车每年能节省 万升汽油,求购买这批混合动力公交车需要多少万元?
万升汽油,求购买这批混合动力公交车需要多少万元?【答案】(1)
 ;(2)购买这批混合动力公交车需要1040万元.
;(2)购买这批混合动力公交车需要1040万元.【解析】
(1)根据“购买一台A型车比购买一台B型车多20万元,购买2台A型车比购买3台B型车少60万元.”即可列出关于a、b的二元一次方程组,解之即可得出结论;
(2)设A型车购买x台,B型车购买y台,根据总节油量=2.4×A型车购买的数量+2.2×B型车购买的数量、A型车数量+B型车数量=10得出方程组,解之求得x和y的值,再根据总费用=120×A型车购买的数量+100×B型车购买的数量即可算出购买这批混合动力公交车的总费用.
解:
 根据题意得:
根据题意得: ,
,解得:
 ;
; 设A型车购买x台,B型车购买y台,
设A型车购买x台,B型车购买y台,根据题意得:
 ,
,解得:
 ,
, 万元
万元 .
.答:购买这批混合动力公交车需要1040万元.
【点睛】
本题考查了二元一次方程组的应用,根据题意找出等量关系列出方程组是解题的关键.
【题型】解答题
【结束】
16【题目】在边长为1的正方形网格中
 作出
作出 关于直线MN对称的
关于直线MN对称的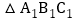 ;
; 若
若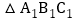 经过图形平移得到
经过图形平移得到 ,当点A的坐标是
,当点A的坐标是 时,请建立适当的直角坐标系,分别写出点
时,请建立适当的直角坐标系,分别写出点 ,
, ,
, 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠BAD=90°,对角线BD⊥DC.

(1)求证:△ABD∽△DCB;
(2)如果AD=4,BC=9,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1的正方形网格中
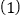 作出
作出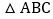 关于直线MN对称的
关于直线MN对称的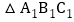 ;
; 若
若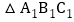 经过图形平移得到
经过图形平移得到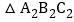 ,当点A的坐标是
,当点A的坐标是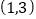 时,请建立适当的直角坐标系,分别写出点
时,请建立适当的直角坐标系,分别写出点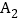 ,
,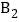 ,
, 的坐标.
的坐标.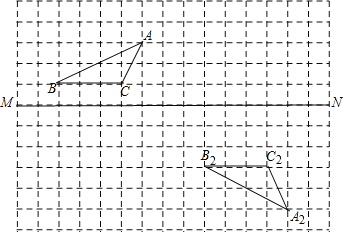
【答案】(1)见解析;(2)
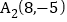 ,
,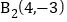 ,
,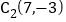 .
.【解析】
(1)直接利用轴对称图形的性质得出对应点位置进而得出答案;
(2)直接利用A点坐标得出平面直角坐标系,进而得出各点坐标.
解:
 如图所示:
如图所示: ,即为所求;
,即为所求;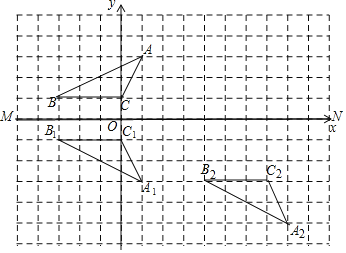
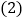 点
点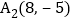 ,
,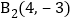 ,
,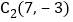 .
.【点睛】
此题主要考查了轴对称变换以及平移变换、根据点的坐标建立平面直角坐标系,正确得出对应点位置是解题关键.
【题型】解答题
【结束】
17【题目】
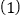 计算:
计算: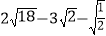 ;
;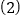 计算:
计算: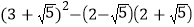 ;
;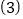 解方程组:
解方程组: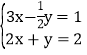 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】《中华人民共和国道路交通管理条例》规定:小汽车在城街路上行驶速度不得超过70 km/h,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面车速检测仪 A的正前方60 m处的C点,过了5 s后,测得小汽车所在的B点与车速检测仪A之间的距离为100 m.
(1)求B,C间的距离.
(2)这辆小汽车超速了吗?请说明理由.

相关试题

