【题目】如图,![]() ,点
,点![]() 在点
在点![]() 的右侧,
的右侧,![]() ,
,![]() 的平分线交于点
的平分线交于点![]() (不与
(不与![]() ,
,![]() 点重合),
点重合),![]() .设
.设![]() .
.

(1)若点![]() 在点
在点![]() 的左侧,求
的左侧,求![]() 的度数(用含
的度数(用含![]() 的代数式表示)
的代数式表示)
(2)将(1)中的线段![]() 沿
沿![]() 方向平移,当点
方向平移,当点![]() 移动到点
移动到点![]() 右侧时,请画出图形并判断
右侧时,请画出图形并判断![]() 的度数是否改变.若改变,请求出
的度数是否改变.若改变,请求出![]() 的度数(用含
的度数(用含![]() 的代数式表示);若不变,请说明理由.
的代数式表示);若不变,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 的度数改变,度数为
的度数改变,度数为![]()
【解析】
(1)过点E作![]() ,根据平行线性质推出∠ABE=∠BEF,∠CDE=∠DEF,根据角平分线定义得出
,根据平行线性质推出∠ABE=∠BEF,∠CDE=∠DEF,根据角平分线定义得出![]() ,∠CDE=
,∠CDE=![]() ∠ADC=35°,求出∠BEF的度数,进而可求出∠ABC的度数;
∠ADC=35°,求出∠BEF的度数,进而可求出∠ABC的度数;
(2)过点E作![]() ,根据角平分线定义得出
,根据角平分线定义得出![]() ,∠CDE=
,∠CDE=![]() ∠ADC=35°,根据平行线性质得出即可.
∠ADC=35°,根据平行线性质得出即可.
(1)如图1,过点![]() 作
作![]() .
.

∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)![]() 的度数改变.
的度数改变.
画出的图形如图2,过点![]() 作
作![]() .
.

∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次安全知识测验中,学生得分均为整数,满分10分,这次测验中甲、乙两组学生人数都为6人,成绩如下(单位:分):
甲:7,9,10,8,5,9;
乙:9,6,8,10,7,8
(1)请补充完整下面的成绩统计分析表:平均分
方差
众数
中位数
甲组
8
9
乙组

8
8
(2)甲组学生说他们的众数高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出一条支持乙组学生观点的理由. . -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车开往距离出发地
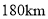 的目的地,出发后第一个小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前
的目的地,出发后第一个小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前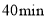 到达目的地,设第一个小时内行驶的速度为
到达目的地,设第一个小时内行驶的速度为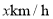 .
.(1)求汽车实际走完全程所花的时间
(2)若按原路返回,司机准备一半路程以
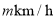 的速度行驶,另一半路程以
的速度行驶,另一半路程以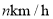 的速度行驶
的速度行驶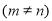 ,朋友建议他一半时间以
,朋友建议他一半时间以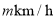 的速度行驶,另一半时间以
的速度行驶,另一半时间以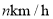 的速度行驶,你觉得谁的方案会更快?请说明理由.
的速度行驶,你觉得谁的方案会更快?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2x﹣m=0有两个实数根.
(1)求实数m的取值范围;
(2)若方程的两个实数根为x1、x2 , 且x1x2=2m2﹣1,求实数m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了保护环境,某公交公司决定购买A、B两种型号的全新混合动力公交车共10辆,其中A种型号每辆价格为a万元,每年节省油量为
 万升;B种型号每辆价格为b万元,每年节省油量为
万升;B种型号每辆价格为b万元,每年节省油量为 万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元. 请求出a和b;
请求出a和b; 若购买这批混合动力公交车每年能节省
若购买这批混合动力公交车每年能节省 万升汽油,求购买这批混合动力公交车需要多少万元?
万升汽油,求购买这批混合动力公交车需要多少万元?【答案】(1)
 ;(2)购买这批混合动力公交车需要1040万元.
;(2)购买这批混合动力公交车需要1040万元.【解析】
(1)根据“购买一台A型车比购买一台B型车多20万元,购买2台A型车比购买3台B型车少60万元.”即可列出关于a、b的二元一次方程组,解之即可得出结论;
(2)设A型车购买x台,B型车购买y台,根据总节油量=2.4×A型车购买的数量+2.2×B型车购买的数量、A型车数量+B型车数量=10得出方程组,解之求得x和y的值,再根据总费用=120×A型车购买的数量+100×B型车购买的数量即可算出购买这批混合动力公交车的总费用.
解:
 根据题意得:
根据题意得: ,
,解得:
 ;
; 设A型车购买x台,B型车购买y台,
设A型车购买x台,B型车购买y台,根据题意得:
 ,
,解得:
 ,
, 万元
万元 .
.答:购买这批混合动力公交车需要1040万元.
【点睛】
本题考查了二元一次方程组的应用,根据题意找出等量关系列出方程组是解题的关键.
【题型】解答题
【结束】
16【题目】在边长为1的正方形网格中
 作出
作出 关于直线MN对称的
关于直线MN对称的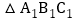 ;
; 若
若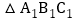 经过图形平移得到
经过图形平移得到 ,当点A的坐标是
,当点A的坐标是 时,请建立适当的直角坐标系,分别写出点
时,请建立适当的直角坐标系,分别写出点 ,
, ,
, 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移2格,再向上平移3格,其中每个格子的边长为1个单位长度。
(1)画出△ABC边AB上的高;
(2)请在图中画出平移后的三角形A’B’C’;
(3)若连接BB′,CC′,则这两条线段之间的关系是_____________________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠BAD=90°,对角线BD⊥DC.

(1)求证:△ABD∽△DCB;
(2)如果AD=4,BC=9,求BD的长.
相关试题

