【题目】我们学习了“圆心角、弧、弦的关系”,实际上我们还可以得到“圆心角、弧、弦、弦心距之间的关系”如下:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距(弦心距指从圆心到弦的距离,如图1中的OC、OC′,弦心距也可以说成圆心到弦的垂线段的长度)中有一组量相等,那么它们对应的其余各组量也相等.请直接运用圆心角、弧、弦、弦心距之间的关系解答下列问题:
如图2,O是∠EPF的平分线上一点,以点O为圆心的圆与角的两边分别交于点A、B、C、D.

(1)求证:AB=CD;
(2)若角的顶点P在圆上,上述结论还成立吗?若不成立,请说明理由;若成立,请加以证明.
参考答案:
【答案】(1)证明见解析;(2)上述结论成立.
【解析】试题分析:(1)过O作OM⊥AB于M,ON⊥CD于N,根据角平分线性质得出ON=OM,再根据题中定义即可得出答案;(2)方法同(1).
解:(1)过O作OM⊥AB于M,ON⊥CD于N,则∠OMB=∠OND=90°.
又∵PO平分∠EPF,∴OM=ON.
∵OM、ON分别是弦AB、CD的弦心距,
∴AB=CD.
(2)上述结论成立.
当点P在⊙O上时,由(1)知OM=ON,
∵OM、ON分别是弦PB、PD的弦心距,
∴PB=PD,即AB=CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在以下现象中:①温度计中,液柱的上升或下降;② 打气筒打气时,活塞的运动;③ 钟摆的摆动;④ 传送带上,瓶装饮料的移动,属于平移的是( )
A. ① ,② B. ①, ③ C. ②, ③ D. ② ,④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,其中点A(-1,0),点C(0,5),点D(1,8)都在抛物线上,已知M为抛物线的顶点.

(1)求抛物线的表达式;
(2)求△MCB的面积;
(3)根据图形直接写出使直线MC表示的一次函数值大于二次函数值的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校园内有一块菱形的空地ABCD,为了美化环境,现要进行绿化,计划在中间建设一个面积为S的矩形绿地EFGH.其中,点E,F,G,H分别在菱形的四条边上,AB=a米,BE=BF=DG=DH=x米,∠A=60°.
(1)求S关于x的函数关系式,并直接写出自变量x的取值范围;
(2)若a=100,求S的最大值,并求出此时x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形有两条边的长度为2和5,则此等腰三角形的周长为( )
A.9
B.12
C.9或12
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在⊙O中,AC、BC是弦,根据条件填空:
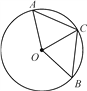
(1)若AC=BC,则________________;
(2)若
 ,则______________;
,则______________;(3)若∠AOC=∠BOC,则______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列的说法中,正确的是 ( )
A. 会重合的图形一定是轴对称图形.
B. 中心对称图形一定是会重合的图形.
C. 两个成中心对称的图形的对称点连线必过对称中心.
D. 两个会重合的三角形一定关于某一点成中心对称.
相关试题

