【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() 是直线
是直线![]() 在第一象限内的一个动点
在第一象限内的一个动点
(1)求⊿![]() 的面积
的面积![]() 与
与![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围?
的取值范围?
(2)过点![]() 作
作![]() 轴于点
轴于点![]() , 作
, 作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,是否存在一点
,是否存在一点![]() 使得
使得![]() 的长最小,若存在,求出
的长最小,若存在,求出![]() 的最小值;若不存在,请说明理由 ?
的最小值;若不存在,请说明理由 ?

参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 的最小值为
的最小值为![]()
【解析】本题的⑴问直接根据坐标来表示⊿![]() 的底边和底边上的高,利用三角形的面积公式得出函数解析式;
的底边和底边上的高,利用三角形的面积公式得出函数解析式;
本题的⑵抓住四边形![]() 是矩形,矩形的对角线相等即
是矩形,矩形的对角线相等即![]() ,从而把
,从而把![]() 转化到
转化到![]() 上来解决,当
上来解决,当![]() 的端点
的端点![]() 运动到
运动到![]() 时
时![]() 最短,以此为切入点,问题可获得解决.
最短,以此为切入点,问题可获得解决.
⑴.∵![]() 的坐标为
的坐标为![]() ,
,![]() 是直线
是直线![]() 在第一象限的一个动点,且
在第一象限的一个动点,且![]() 轴.
轴.
∴![]() ,
,![]()
∴![]() 整理得:
整理得:![]()
自变量![]() 的取值范围是:
的取值范围是:![]()
⑵. 存在一点![]() 使得
使得![]() 的长最小.
的长最小.
求出直线![]() 与
与![]() 轴交点的坐标为
轴交点的坐标为![]() , 与
, 与![]() 轴交点的坐标为
轴交点的坐标为![]()
∴![]() ∴
∴![]()
根据勾股定理计算:![]() .
.
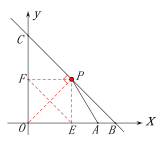
∵![]() 轴,
轴, ![]() 轴,
轴,![]() 轴
轴![]()
![]() 轴
轴
∴![]()
∴四边形![]() 是矩形 ∴
是矩形 ∴![]()
当![]() 的端点
的端点![]() 运动到
运动到![]() (实际上点
(实际上点![]() 恰好是
恰好是![]() 的中点)时
的中点)时
的![]() 最短(垂线段最短)(见示意图)
最短(垂线段最短)(见示意图)
又∵![]() ∴
∴![]() 点为线段
点为线段![]() 中点(三线合一)
中点(三线合一)
∴ ![]() (注:也可以用面积方法求解)
(注:也可以用面积方法求解)
∴![]() 即
即![]() 的最小值为
的最小值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的数阵是由77个偶数排成:

(1)如图中任意作一个平行四边形框,设左上角的数为x,那么其他3个数从小到大可分别表示为 .
(2)小红说这4个数的和是292,能求出这4个数吗?若存在,请求出这4个数.不存在说明理由.
(3)小明说4个数的和是420,存在这样的数吗?若存在,请求出这4个数,不存在说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】骰子是一种特别的数字立方体(见下图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:德国著名数学家高斯被认为是历史上最重要的数学家之一,并有"数学王子"的美誉.高斯从小就善于观察和思考.在他读小学时候就能在课堂上快速的计算出
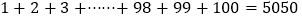 ,今天我们可以将高斯的做法归纳如下:
,今天我们可以将高斯的做法归纳如下:令
 ①
①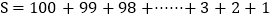 ②
②(右边相加100+1=2+99=3+98=…..=100+1共100组)
①+②:有2S=101x100 解得:
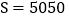
(1)请参照以上做法,回答,3+5+7+9+…..+97= ;
请尝试解决下列问题:
如下图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.

(2)填写下表:
层数
1
2
3
4
该层对应的点数
1
6
12
18
所有层的总点数的和
1
7
19
①写出第n层所对应的点数;(n≥2)
②如果某一层共96个点,求它是第几层;
③写出n层的六边形点阵的总点数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=
 AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( ) 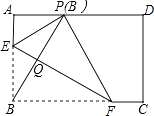
A.①②
B.②③
C.①③
D.①④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 内任取一点
内任取一点 ,连接
,连接 ,在⊿
,在⊿ 外分别以
外分别以 为边作正方形
为边作正方形 和
和 .
.⑴.按题意,在图中补全符合条件的图形;
⑵.连接
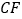 ,求证:⊿
,求证:⊿ ≌⊿
≌⊿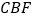 ;
;⑶.在补全的图形中,求证:
 ∥
∥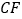 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,……按此规律,则第50个图形中面积为1的正方形的个数为( )

A. 1322 B. 1323 C. 1324 D. 1325
相关试题

