【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE= ![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( ) 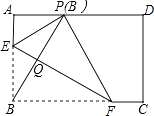
A.①②
B.②③
C.①③
D.①④
参考答案:
【答案】D
【解析】解:∵AE= ![]() AB, ∴BE=2AE,
AB, ∴BE=2AE,
由翻折的性质得,PE=BE,
∴∠APE=30°,
∴∠AEP=90°﹣30°=60°,
∴∠BEF= ![]() (180°﹣∠AEP)=
(180°﹣∠AEP)= ![]() (180°﹣60°)=60°,
(180°﹣60°)=60°,
∴∠EFB=90°﹣60°=30°,
∴EF=2BE,故①正确;
∵BE=PE,
∴EF=2PE,
∵EF>PF,
∴PF<2PE,故②错误;
由翻折可知EF⊥PB,
∴∠EBQ=∠EFB=30°,
∴BE=2EQ,EF=2BE,
∴FQ=3EQ,故③错误;
由翻折的性质,∠EFB=∠EFP=30°,
∴∠BFP=30°+30°=60°,
∵∠PBF=90°﹣∠EBQ=90°﹣30°=60°,
∴∠PBF=∠PFB=60°,
∴△PBF是等边三角形,故④正确;
综上所述,结论正确的是①④.
故选:D.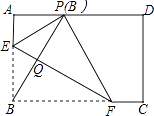
求出BE=2AE,根据翻折的性质可得PE=BE,再根据直角三角形30°角所对的直角边等于斜边的一半求出∠APE=30°,然后求出∠AEP=60°,再根据翻折的性质求出∠BEF=60°,根据直角三角形两锐角互余求出∠EFB=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半可得EF=2BE,判断出①正确;利用30°角的正切值求出PF= ![]() PE,判断出②错误;求出BE=2EQ,EF=2BE,然后求出FQ=3EQ,判断出③错误;求出∠PBF=∠PFB=60°,然后得到△PBF是等边三角形,判断出④正确.
PE,判断出②错误;求出BE=2EQ,EF=2BE,然后求出FQ=3EQ,判断出③错误;求出∠PBF=∠PFB=60°,然后得到△PBF是等边三角形,判断出④正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】骰子是一种特别的数字立方体(见下图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:德国著名数学家高斯被认为是历史上最重要的数学家之一,并有"数学王子"的美誉.高斯从小就善于观察和思考.在他读小学时候就能在课堂上快速的计算出
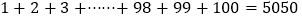 ,今天我们可以将高斯的做法归纳如下:
,今天我们可以将高斯的做法归纳如下:令
 ①
①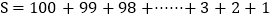 ②
②(右边相加100+1=2+99=3+98=…..=100+1共100组)
①+②:有2S=101x100 解得:
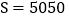
(1)请参照以上做法,回答,3+5+7+9+…..+97= ;
请尝试解决下列问题:
如下图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.

(2)填写下表:
层数
1
2
3
4
该层对应的点数
1
6
12
18
所有层的总点数的和
1
7
19
①写出第n层所对应的点数;(n≥2)
②如果某一层共96个点,求它是第几层;
③写出n层的六边形点阵的总点数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与
与 轴、
轴、 轴分别交于
轴分别交于 ,点
,点 的坐标为
的坐标为 ,
, 是直线
是直线 在第一象限内的一个动点
在第一象限内的一个动点(1)求⊿
 的面积
的面积 与
与 的函数解析式,并写出自变量
的函数解析式,并写出自变量 的取值范围?
的取值范围?(2)过点
 作
作 轴于点
轴于点 , 作
, 作 轴于点
轴于点 ,连接
,连接 ,是否存在一点
,是否存在一点 使得
使得 的长最小,若存在,求出
的长最小,若存在,求出 的最小值;若不存在,请说明理由 ?
的最小值;若不存在,请说明理由 ?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
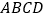 内任取一点
内任取一点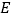 ,连接
,连接 ,在⊿
,在⊿ 外分别以
外分别以 为边作正方形
为边作正方形 和
和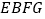 .
.⑴.按题意,在图中补全符合条件的图形;
⑵.连接
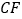 ,求证:⊿
,求证:⊿ ≌⊿
≌⊿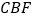 ;
;⑶.在补全的图形中,求证:
 ∥
∥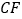 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,……按此规律,则第50个图形中面积为1的正方形的个数为( )

A. 1322 B. 1323 C. 1324 D. 1325
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-16-(-1+
 )÷3×[2-(-4)2]
)÷3×[2-(-4)2](2)解方程:
 -
-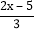 =-1
=-1(3)先化简,再求值:2(x2-2xy)+[2y2-3(x2-2xy+y2)+x2],其中x=1,y=-
 .
.
相关试题

