【题目】如图正方形ABCD的边长为4,E、F分别为DC、BC中点. 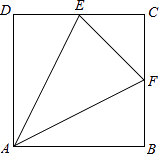
(1)求证:△ADE≌△ABF.
(2)求△AEF的面积.
参考答案:
【答案】
(1)证明:∵四边形ABCD为正方形,
∴AB=AD,∠D=∠B=90°,DC=CB,
∵E、F为DC、BC中点,
∴DE= ![]() DC,BF=
DC,BF= ![]() BC,
BC,
∴DE=BF,
在△ADE和△ABF中,
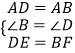 ,
,
∴△ADE≌△ABF(SAS)
(2)解:由题知△ABF、△ADE、△CEF均为直角三角形,
且AB=AD=4,DE=BF= ![]() ×4=2,CE=CF=
×4=2,CE=CF= ![]() ×4=2,
×4=2,
∴S△AEF=S正方形ABCD﹣S△ADE﹣S△ABF﹣S△CEF
=4×4﹣ ![]() ×4×2﹣
×4×2﹣ ![]() ×4×2﹣
×4×2﹣ ![]() ×2×2
×2×2
=6
【解析】(1)由四边形ABCD为正方形,得到AB=AD,∠B=∠D=90°,DC=CB,由E、F分别为DC、BC中点,得出DE=BF,进而证明出两三角形全等;(2)首先求出DE和CE的长度,再根据S△AEF=S正方形ABCD﹣S△ADE﹣S△ABF﹣S△CEF得出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C′与AB相交于点D,则C′D= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=﹣
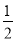 x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.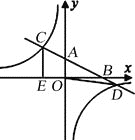
(1)求反比例函数的解析式;
(2)连接OD,求△OBD的面积.
-
科目: 来源: 题型:
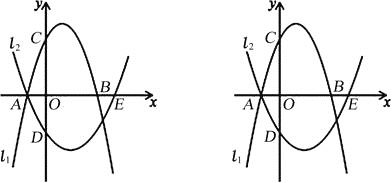
查看答案和解析>>【题目】已知抛物线l1:y=﹣x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2).
(1)求抛物线l2的解析式;
(2)点P为线段AB上一动点(不与A、B重合),过点P作y轴的平行线交抛物线l1于点M,交抛物线l2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b是一元二次方程x2+x﹣4=0的两个不相等的实数根,则a2﹣b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具商店销售功能相同的A、B两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器5个以上超出部分按原价的七折销售,设购买x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过5个,购买哪种品牌的计算器更合算?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1 , 再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2 , 如此进行下去,得到四边形AnBnCnDn .
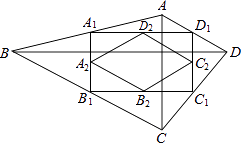
(1)求证:四边形A1B1C1D1是矩形;
(2)四边形A3B3C3D3是形;
(3)四边形A1B1C1D1的周长为;
(4)四边形AnBnCnDn的面积为 .
相关试题

