Question

【题目】如图，3×3的方格分为上中下三层，第一层有一枚黑色方块甲，可在方格A、B、C中移动，第二层有两枚固定不动的黑色方块，第三层有一枚黑色方块乙，可在方格D、E、F中移动，甲、乙移入方格后，四枚黑色方块构成各种拼图．

（1）若乙固定在E处，移动甲后黑色方块构成的拼图是轴对称图形的概率是________．

（2）若甲、乙均可在本层移动．

①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率________．

②黑色方块所构拼图是中心对称图形的概率是________．

Answer 1

【答案】（1）；（2）①；②.

【解析】

（1）由乙固定在E处，移动甲后黑色方块构成的拼图一共有3种可能，其中有两种情形是轴对称图形，所以若乙固定在E处，移动甲后黑色方块构成的拼图是轴对称图形的概率是；（2）①由树状图得到黑色方块所构拼图是轴对称图形的概率；②黑色方块所构拼图中是中心对称图形有两种情形，①甲在B处，乙在F处，②甲在C处，乙在E处，所以黑色方块所构拼图是中心对称图形的概率是．

（1）若乙固定在E处，移动甲后黑色方块构成的拼图一共有3种可能，其中有两种情形是轴对称图形，所以若乙固定在E处，移动甲后黑色方块构成的拼图是轴对称图形的概率是 ．

故答案为．（2）①由树状图可知，黑色方块所构拼图是轴对称图形的概率= ．

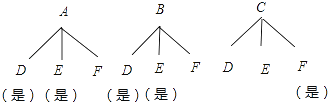
②黑色方块所构拼图中是中心对称图形有两种情形，

甲在B处，乙在F处或甲在C处，乙在E处，

所以黑色方块所构拼图是中心对称图形的概率是 ．

故答案为 ．