【题目】如图,AB是⊙O的直径,直线EF切⊙O于点C, AD⊥EF于点D.
(1)求证:AC平分∠BAD;
(2)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.(结果保留π)
参考答案:
【答案】
(1)证明:连接OC, ![]() 直线EF切
直线EF切 ![]() 于点C,
于点C, ![]()
![]()
![]()
![]()
![]()
![]()
![]() 即
即 ![]() 平分
平分 ![]() ;
;
(2)解: ![]()
![]()
![]()
![]() 是等边三角形,
是等边三角形, ![]() 的半径为2,
的半径为2, ![]()
![]() 在
在 ![]() 中,
中, ![]() 由勾股定理得
由勾股定理得 ![]()
![]()
![]()
【解析】(1)抓住已知直线EF切⊙O于点C,因此连接OC,得出O C ⊥ E F , 根据 AD⊥EF,易得到OC∥AD,得出∠OCA=∠DAC,再根据同圆的半径相等及等量代换,易证得结论。
(2)观察图形可知S阴影=S梯形OCDAS扇形OCA,根据已知求出∠AOC的度数、AD、CD的长,即可求得结果。
【考点精析】关于本题考查的平行线的判定与性质和切线的性质定理,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.

(1)求证:AE是⊙O的切线;
(2)当BC=4时求劣弧AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在《朗读者》节目的影响下,某中学开展了“好书伴我成长”读书活动.为了解5月份八年级300名学生的读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:
册数
0
1
2
3
4
人数
3
13
16
17
1
关于这组数据,下列说法正确的是 ( )
A. 中位数是2 B. 众数是17 C. 平均数是3 D. 方差是2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图案中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(6,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△AOB的顶点O与原点重合,直角顶点A在x轴上,顶点B的坐标为(4,3),直线
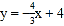 与x轴、y轴分别交于点D、E,交OB于点F.
与x轴、y轴分别交于点D、E,交OB于点F. (1)写出图中的全等三角形及理由;
(2)求OF的长.

相关试题

