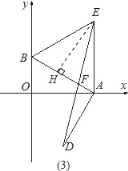
【题目】如图，平面直角坐标系中，点A、B分别在x、y轴上，点B的坐标为（0，1），∠BAO=30°．

（1）求AB的长度；

（2）以AB为一边作等边△ABE，作OA的垂直平分线MN交AB的垂线AD于点D．求证：BD=OE；

（3）在（2）的条件下，连接DE交AB于F．求证：F为DE的中点．

参考答案：

【答案】（1）2；（2）详见解析；（3）详见解析.

【解析】

（1）直接运用直角三角形30°角的性质即可．
（2）连接OD，易证△ADO为等边三角形，再证△ABD≌△AEO即可．
（3）作EH⊥AB于H，先证△ABO≌△AEH，得AO=EH，再证△AFD≌△EFH即可．

（1）解：∵在Rt△ABO中，∠BAO=30°，

∴AB=2BO=2；

（2）证明：连接OD，

∵△ABE为等边三角形，

∴AB=AE，∠EAB=60°，

∵∠BAO=30°，作OA的垂直平分线MN交AB的垂线AD于点D，

∴∠DAO=60°．

∴∠EAO=∠NAB

又∵DO=DA，

∴△ADO为等边三角形．

∴DA=AO．

在△ABD与△AEO中，

∵，

∴△ABD≌△AEO（SAS）．

∴BD=OE．

（3）证明：作EH⊥AB于H．

∵AE=BE，∴AH=AB，

∵BO=AB，∴AH=BO，

在Rt△AEH与Rt△BAO中，

，

∴Rt△AEH≌Rt△BAO（HL），

∴EH=AO=AD．

又∵∠EHF=∠DAF=90°，

在△HFE与△AFD中，

，

∴△HFE≌△AFD（AAS），

∴EF=DF．

∴F为DE的中点．

关闭