【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标系分别为A(-2,1),B(-1,4),C(-3,-2)
(1)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A1B1C1 , 并直接写出C1点坐标;
(2)如果点D(a , b)在线段AB上,请直接写出经过(1)的变化后点D的对应点D1的坐标.
参考答案:
【答案】
(1)
解:如图所示:△A1B1C1即为所求,C1点坐标为(-6,4);
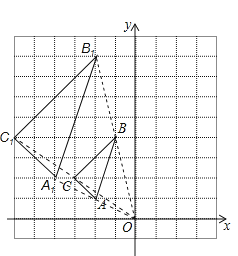
(2)
解:如果点D(a,b)在线段AB上,经过(1)的变化后点D的对应点D1的坐标为;(2a,2b).
【解析】(1)利用位似比为1:2,进而将各对应点坐标扩大为原来的2倍,进而得出答案;(2)利用(1)中位似比得出对应点坐标关系.
【考点精析】解答此题的关键在于理解作图-位似变换的相关知识,掌握对应点到位似中心的距离比就是位似比,对应线段的比等于位似比,位似比也有顺序;已知图形的位似图形有两个,在位似中心的两侧各有一个.位似中心,位似比是它的两要素.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD与四边形AEFG是位似图形,且AC:AF=2:3,则下列结论不正确的是( )

A.四边形ABCD与四边形AEFG是相似图形
B.AD与AE的比是2:3
C.四边形ABCD与四边形AEFG的周长比是2:3
D.四边形ABCD与四边形AEFG的面积比是4:9 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,1),B(-2,0),以坐标原点O为位似中心,将线段AB放大2倍,放大后的线段A′B′与线段AB在同一侧,则两个端点A′,B′的坐标分别为.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.

(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(3,0),B(4,4),C(-2,3),将点O , A , B , C的横坐标、纵坐标都乘以-2.

(1)画出以变化后的四个点为顶点的四边形;
(2)由(1)得到的四边形与四边形OABC位似吗?如果位似,指出位似中心及与原图形的相似比. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.
(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F.求证:F为DE的中点.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.

(1)画出位似中心点O;
(2)直接写出△ABC与△A′B′C′的位似比;
(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A′B′C′关于点O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.
相关试题

