搜索
【题目】如图，AB=AC，∠BAC=120°，AB的垂直平分线交BC于点D，那么∠DAC的度数为（ ）
A. 90° B. 80° C. 70° D. 60°
参考答案：
【答案】A
【解析】试题分析：由AB=AC，∠BAC=120°，根据等腰三角形的性质得到∠B=∠C，利用三角形内角和定理得到∠B=
（180°﹣120°）=30°，然后根据线段垂直平分线的性质得到
DB=DA，则∠BAD=∠B=30°，再根据∠DAC=∠BAC﹣∠BAD进行计算．
解：∵AB=AC，∠BAC=120°，
∴∠B=∠C，
∴∠B=（180°﹣120°）=30°，
∵AB的垂直平分线交BC于点D，
∴DB=DA，
∴∠BAD=∠B=30°，
∴∠DAC=∠BAC﹣∠BAD=120°﹣30°=90°．
故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，O为数轴的原点，A，B为数轴上的两点，点A表示的数为－30，点B表示的数为100.
(1)A，B两点间的距离是________．
(2)若点C也是数轴上的点，点C到点B的距离是点C到原点O的距离的3倍，求点C表示的数．
(3)若电子蚂蚁P从点B出发，以6个单位长度/s的速度向左运动，同时另一只电子蚂蚁Q恰好从点A出发，以4个单位长度/s的速度向左运动，设两只电子蚂蚁同时运动到了数轴上的点D，那么点D表示的数是多少？
(4)若电子蚂蚁P从点B出发，以8个单位长度/s的速度向右运动，同时另一只电子蚂蚁Q恰好从点A出发，以4个单位长度/s的速度向右运动．设数轴上的点N到原点O的距离等于点P到原点O的距离的一半(点N在原点右侧)，有下面两个结论：①ON＋AQ的值不变；②ON－AQ的值不变，请判断哪个结论正确，并求出正确结论的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】先化简，再求值：
(1)3x2－
，其中x＝2；(2)(－3xy－7y)＋[4x－3(xy＋y－2x)]，其中xy＝－2，x－y＝3.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠C＝90°，∠A＝30°.分别以顶点A，B为圆心，大于
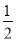AB的长为半径作弧，两弧在直线AB两侧分别交于M，N两点，过M，N作直线交AB于点P，交AC于点D，连结BD.下列结论中，错误的是( )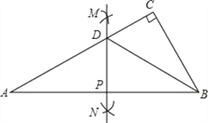
A. 直线AB是线段MN的垂直平分线 B. CD＝
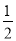ADC. BD平分∠ABC D. S△APD＝S△BCD
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在等腰△ABC中，AB=AC，∠BAC=50°．∠BAC的平分线与线段AB的中垂线交于点O，点C沿EF折叠后与点O重合，则∠AOF的度数是（ ）
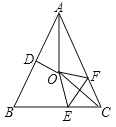
A．105° B．110° C．115° D．120°
-
科目： 来源： 题型：
查看答案和解析>>【题目】有理数a，b，c在数轴上的位置如图所示，且表示数a的点、数b的点与原点的距离相等．
(1)用“＞”“＜”或“＝”填空：b______0，a＋b______0，a－c______0，b－c______0；
(2)|b－1|＋|a－1|＝________；
(3)化简：|a＋b|＋|a－c|－|b|＋|b－c|.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一个不透明的箱子里，装有黄、白、黑各一个球，它们除了颜色之外没有其他区别，随机从箱子里取出1个球，放回搅匀再取一次，请你用画树状图或列表的方法表示所有可能出现的结果，求两次取出的都是白球的概率．
相关试题
