【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.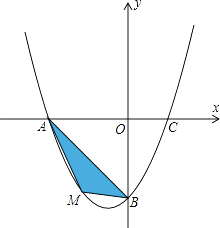
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.
求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
参考答案:
【答案】
(1)解:设此抛物线的函数解析式为:
y=ax2+bx+c(a≠0),
将A(﹣4,0),B(0,﹣4),C(2,0)三点代入函数解析式得:
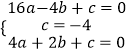
解得 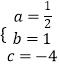 ,
,
所以此函数解析式为:y= ![]()
(2)解:∵M点的横坐标为m,且点M在这条抛物线上,
∴M点的坐标为:(m, ![]() ),
),
∴S=S△AOM+S△OBM﹣S△AOB
= ![]() ×4×(﹣
×4×(﹣ ![]() m2﹣m+4)+
m2﹣m+4)+ ![]() ×4×(﹣m)﹣
×4×(﹣m)﹣ ![]() ×4×4
×4×4
=﹣m2﹣2m+8﹣2m﹣8
=﹣m2﹣4m,
=﹣(m+2)2+4,
∵﹣4<m<0,
当m=﹣2时,S有最大值为:S=﹣4+8=4.
答:m=﹣2时S有最大值S=4
(3)解:设P(x, ![]() x2+x﹣4).
x2+x﹣4).
当OB为边时,根据平行四边形的性质知PQ∥OB,且PQ=OB,
∴Q的横坐标等于P的横坐标,
又∵直线的解析式为y=﹣x,
则Q(x,﹣x).
由PQ=OB,得|﹣x﹣( ![]() x2+x﹣4)|=4,
x2+x﹣4)|=4,
解得x=0,﹣4,﹣2±2 ![]() .
.
x=0不合题意,舍去.
如图,当BO为对角线时,知A与P应该重合,OP=4.四边形PBQO为平行四边形则BQ=OP=4,Q横坐标为4,代入y=﹣x得出Q为(4,﹣4).
由此可得Q(﹣4,4)或(﹣2+2 ![]() ,2﹣2
,2﹣2 ![]() )或(﹣2﹣2
)或(﹣2﹣2 ![]() ,2+2
,2+2 ![]() )或(4,﹣4).
)或(4,﹣4).

【解析】(1)利用待定系数法,把ABC三点坐标代入解析式即可求出;(2)最值问题的基本解决策略就是函数思想,设出M的横坐标为m,作为自变量,△AMB的面积为S为函数,由已知得S=S△AOM+S△OBM﹣S△AOB,分别用m的代数式表示各三角形面积,构建出二次函数,运用配方法求出最大值;(3)可分类讨论:OB为边,根据平行四边形的性质知PQ∥OB,且PQ=OB,构建方程|﹣x﹣( 1 2 x2+x﹣4)|=4;当BO为对角线时,A与P应该重合,OP=4.四边形PBQO为平行四边形,则BQ=OP=4,进而求出坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】南通某校为了了解家长和学生参与南通安全教育平台“
 防灾减灾”专题教育活动的情况,在本校学生中随机抽取部分学生做调查,把收集的数据分为以下
防灾减灾”专题教育活动的情况,在本校学生中随机抽取部分学生做调查,把收集的数据分为以下 类情形:
类情形:A.仅学生自己参与;
B.家长和学生一起参与;
C.仅家长参与;
D.家长和学生都未参与
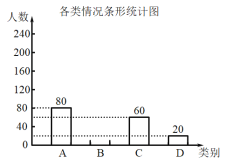
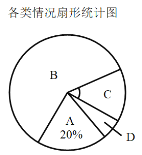
请根据上图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了多少名学生?
(2)补全条形统计图,并在扇形统计图中计算
 类所对应扇形的圆心角的度数;
类所对应扇形的圆心角的度数;(3)根据抽样调查结果,估计该校
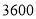 名学生中“家长和学生都未参与”的人数.
名学生中“家长和学生都未参与”的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.

(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为1,求图中阴影部分的面积(结果保留π) -
科目: 来源: 题型:
查看答案和解析>>【题目】在南通市中小学标准化建设工程中,某校计划购进一批电脑和电子白板,经过市场考察得知,购买
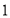 台电脑和
台电脑和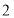 台电子白板需要
台电子白板需要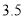 万元,购买
万元,购买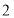 台电脑和
台电脑和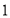 台电子白板需要
台电子白板需要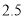 万元.
万元.(1)求每台电脑、每台电子白板各多少万元;
(2)根据学校实际,需购进电脑和电子白板共
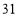 台,若总费用不超过
台,若总费用不超过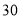 万元,则至多购买电子白板多少台?
万元,则至多购买电子白板多少台? -
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑自行车上学,路上要经过平路、上坡、下坡、平路,小明下坡、上坡及平路速度均为匀速,但上坡速度最慢,下坡速度最快,那么小明骑自行车上学时,离开家的路程
 与所用时间
与所用时间 的函数图象大致是( ).
的函数图象大致是( ).A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一列从小到大,按某种规律排列的数如下:
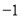 ,3,7,□,15,19,23,□,31,35,□,…,第
,3,7,□,15,19,23,□,31,35,□,…,第 (
( 为正整数)个数记作
为正整数)个数记作 ,
, 是
是 的函数,则
的函数,则 的值可能是下列个数中的( ).
的值可能是下列个数中的( ).A.158B.124C.79D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
 、
、 的坐标分别为
的坐标分别为 ,
, ,其中
,其中 ,
, 满足
满足 .将点
.将点 向右平移
向右平移 个单位长度得到点
个单位长度得到点 ,如图所示.
,如图所示.
(1)求点
 ,
, ,
, 的坐标;
的坐标;(2)动点
 从点
从点 出发,沿着线段
出发,沿着线段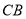 、线段
、线段 以
以 个单位长度/秒的速度运动,同时点
个单位长度/秒的速度运动,同时点 从点
从点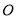 出发沿着线段
出发沿着线段 以
以 个单位长度秒的速度运动,设运动时间为
个单位长度秒的速度运动,设运动时间为 秒
秒 .当
.当 时,求
时,求 的取值范围;是否存在一段时间,使得
的取值范围;是否存在一段时间,使得 ?若存在,求出
?若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
相关试题

