【题目】如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为1,求图中阴影部分的面积(结果保留π)
参考答案:
【答案】
(1)解:直线CD与⊙O相切.理由如下:
如图,连接OD
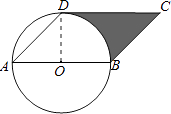
∵OA=OD,∠DAB=45°,
∴∠ODA=45°
∴∠AOD=90°
∵CD∥AB
∴∠ODC=∠AOD=90°,即OD⊥CD
又∵点D在⊙O上,∴直线CD与⊙O相切
(2)解:∵⊙O的半径为1,AB是⊙O的直径,
∴AB=2,
∵BC∥AD,CD∥AB
∴四边形ABCD是平行四边形
∴CD=AB=2
∴S梯形OBCD= ![]() =
= ![]() =
= ![]() ;
;
∴图中阴影部分的面积等于S梯形OBCD﹣S扇形OBD= ![]() ﹣
﹣ ![]() ×π×12=
×π×12= ![]() ﹣
﹣ ![]() .
.
【解析】(1)连接半径,证明出∠ODC=90°,即OD⊥CD即可;(2)阴影部分面积可转化为S梯形OBCD﹣S扇形OBD,可证出四边形ABCD是平行四边形,转化CD=AB=2,分别求出二者面积,作差即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 把解集表示在数轴上,并求出不等式组的整数解.
把解集表示在数轴上,并求出不等式组的整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,有若干个横、纵坐标均为整数的点,按如下顺序依次排列为
 ,
, ,
, ,
, ,
, ,
, 根据这个规律,第
根据这个规律,第 个点的坐标为( )
个点的坐标为( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】南通某校为了了解家长和学生参与南通安全教育平台“
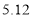 防灾减灾”专题教育活动的情况,在本校学生中随机抽取部分学生做调查,把收集的数据分为以下
防灾减灾”专题教育活动的情况,在本校学生中随机抽取部分学生做调查,把收集的数据分为以下 类情形:
类情形:A.仅学生自己参与;
B.家长和学生一起参与;
C.仅家长参与;
D.家长和学生都未参与
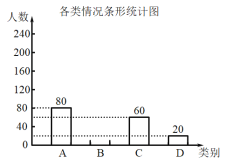
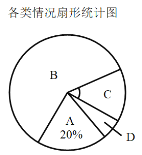
请根据上图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了多少名学生?
(2)补全条形统计图,并在扇形统计图中计算
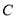 类所对应扇形的圆心角的度数;
类所对应扇形的圆心角的度数;(3)根据抽样调查结果,估计该校
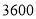 名学生中“家长和学生都未参与”的人数.
名学生中“家长和学生都未参与”的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在南通市中小学标准化建设工程中,某校计划购进一批电脑和电子白板,经过市场考察得知,购买
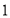 台电脑和
台电脑和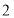 台电子白板需要
台电子白板需要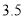 万元,购买
万元,购买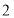 台电脑和
台电脑和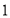 台电子白板需要
台电子白板需要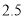 万元.
万元.(1)求每台电脑、每台电子白板各多少万元;
(2)根据学校实际,需购进电脑和电子白板共
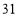 台,若总费用不超过
台,若总费用不超过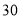 万元,则至多购买电子白板多少台?
万元,则至多购买电子白板多少台? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
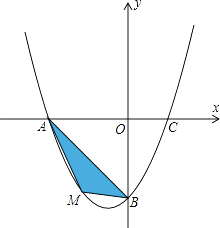
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.
求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑自行车上学,路上要经过平路、上坡、下坡、平路,小明下坡、上坡及平路速度均为匀速,但上坡速度最慢,下坡速度最快,那么小明骑自行车上学时,离开家的路程
 与所用时间
与所用时间 的函数图象大致是( ).
的函数图象大致是( ).A.
 B.
B. C.
C. D.
D.
相关试题

