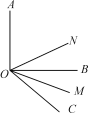
【题目】(1)如图,∠AOB=90°,∠BOC=40°,ON平分∠AOC,OM平分∠BOC,求∠MON的度数;
(2)如果(1)中∠BOC=α,且α<90°,其他条件不变,求∠MON的度数;
(3)如果(1)中∠AOB=β,且β<90°,其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果中能得到什么规律?
参考答案:
【答案】(1)45°(2)45°(3)![]() β(4)∠MON的大小只与∠AOB的大小有关,且∠MON=
β(4)∠MON的大小只与∠AOB的大小有关,且∠MON=![]() ∠AOB
∠AOB
【解析】
(1)根据角平分线的定义得到∠MOC=![]() ∠BOC,∠NOC=
∠BOC,∠NOC=![]() ∠AOC,则∠MON=∠NOC-∠MOC=
∠AOC,则∠MON=∠NOC-∠MOC=![]() (∠AOC-∠BOC)=
(∠AOC-∠BOC)=![]() ∠AOB,然后把∠AOB的度数代入计算即可;
∠AOB,然后把∠AOB的度数代入计算即可;
(2)根据角平分线的定义得到∠MOC=![]() ∠BOC,∠NOC=
∠BOC,∠NOC=![]() ∠AOC,则∠MON=∠NOC-∠MOC=
∠AOC,则∠MON=∠NOC-∠MOC=![]() (∠AOC-∠BOC)=
(∠AOC-∠BOC)=![]() ∠AOB,然后把∠AOB的度数代入计算即可;
∠AOB,然后把∠AOB的度数代入计算即可;
(3)先得到∠AOC=β+ BOC,再根据角平分线的定义得到∠COM=![]() ∠BOC,∠CON=
∠BOC,∠CON=![]() ∠AOC=
∠AOC=![]() (β+ BOC),然后利用∠MON=∠CON-∠COM进行计算;
(β+ BOC),然后利用∠MON=∠CON-∠COM进行计算;
(4)利用前面计算的结论得到∠MON=![]() ∠AOB.
∠AOB.
(1)∠MON=∠NOC-∠MOC=![]() ∠AOC-
∠AOC-![]() ∠BOC=
∠BOC=![]() (∠AOB+∠BOC)-
(∠AOB+∠BOC)-![]() ∠BOC=
∠BOC=![]() ∠AOB=
∠AOB=![]() ×90°=45°;
×90°=45°;
(2)∠MON=∠NOC-∠MOC=![]() ∠AOC-
∠AOC-![]() ∠BOC=
∠BOC=![]() (∠AOB+∠BOC)-
(∠AOB+∠BOC)-![]() ∠BOC=
∠BOC=![]() ∠AOB=
∠AOB=![]() ×90°=45°;
×90°=45°;
(3)∠MON=∠NOC-∠MOC=![]() ∠AOC-
∠AOC-![]() ∠BOC=
∠BOC=![]() (∠AOB+∠BOC)-
(∠AOB+∠BOC)-![]() ∠BOC=
∠BOC=![]() ∠AOB=
∠AOB=![]() β;
β;
(4)∠MON的大小只与∠AOB的大小有关,且∠MON=![]() ∠AOB.
∠AOB.
-
科目: 来源: 题型:
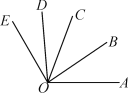
查看答案和解析>>【题目】如图,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOC=70°,∠COE=50°,那么∠BOD是多少度?
(2)如果∠BOD=70°,那么∠AOE是多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形 ABCD 中,AB⊥AD,BC⊥DC,点 M、N 分别是 AB、BC 边上的动点,∠B=56°.当△DMN 的周长最小时,则∠MDN 的度数是_____

-
科目: 来源: 题型:
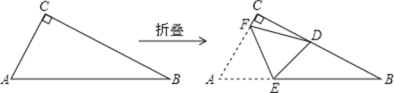
查看答案和解析>>【题目】直角三角形纸片 ABC 中,∠ACB=90°,AC≤BC.如图,将纸片沿某条直线折叠,使点 A 落在直角边 BC 上,记落点为 D.设折痕与 AB、AC 边分别交于点 E、点 F,当折叠后的△CDF 与△BDE 均为等腰三角形,那么纸片中∠B 的度数是_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1) [(x-y)2+(x+y)(x-y)]÷2x,其中 x=3,y=-2
(2)已知
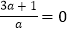 ,求
,求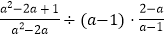 的值.
的值. -
科目: 来源: 题型:
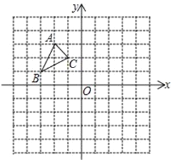
查看答案和解析>>【题目】如图,△ABC 中,A(-2,3)、B(-3,1)、C(-1,2)
(1)作△ABC 关于直线 x=1 对称的图形△A1B1C1,写出三顶点 A1、B1、C1的坐标
(2)在 x 轴上求作一点 D,使四边形 ABDC 的周长最小(保留作图痕迹,不要求写作法和证明)
相关试题

