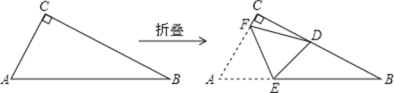
【题目】直角三角形纸片 ABC 中,∠ACB=90°,AC≤BC.如图,将纸片沿某条直线折叠,使点 A 落在直角边 BC 上,记落点为 D.设折痕与 AB、AC 边分别交于点 E、点 F,当折叠后的△CDF 与△BDE 均为等腰三角形,那么纸片中∠B 的度数是_____
参考答案:
【答案】45![]() 或30
或30![]() .
.
【解析】
因为△CDF中,∠C=90![]() ,且△CDF是等腰三角形,所CF=CD.所以∠CFD=∠CDF=45
,且△CDF是等腰三角形,所CF=CD.所以∠CFD=∠CDF=45![]() .设∠DAE=x
.设∠DAE=x![]() ,由对称性可知,AF=FD,AE=DE,所以∠FDA=
,由对称性可知,AF=FD,AE=DE,所以∠FDA=![]() ∠CFD=22.5
∠CFD=22.5![]() ,∠DEB=2 x
,∠DEB=2 x![]() .
.
分DE=DB;BD=BE;DE=BE三种情况讨论可得∠B的度数.
解:因为△CDF中,∠C=90![]() ,且△CDF是等腰三角形,所CF=CD.所以∠CFD=∠CDF=45
,且△CDF是等腰三角形,所CF=CD.所以∠CFD=∠CDF=45![]() .设∠DAE=x
.设∠DAE=x![]() ,由对称性可知,AF=FD,AE=DE,所以∠FDA=
,由对称性可知,AF=FD,AE=DE,所以∠FDA=![]() ∠CFD=22.5
∠CFD=22.5![]() ,∠DEB=2 x
,∠DEB=2 x![]() .分类如下:
.分类如下:
当DE=DB时,∠B=∠DEB=2 x![]() .由∠CDE=∠DEB+∠B得45+22.5+x=4x.解得:x=22.5,此时∠B =45
.由∠CDE=∠DEB+∠B得45+22.5+x=4x.解得:x=22.5,此时∠B =45![]() .图形见图(1).
.图形见图(1).
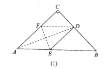
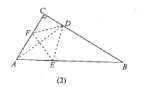
当BD=BE时.则∠B=180![]() -4x
-4x![]() .由∠CDE=∠DEB+∠B得45+22.5+x=2x+180-4x.
.由∠CDE=∠DEB+∠B得45+22.5+x=2x+180-4x.
解得:x=37.5.此时∠B=180![]() -4
-4![]() 37.5=30
37.5=30![]() ,图形见图(2).
,图形见图(2).
当DE=BE时,则∠B=(![]() )
)![]() ,由∠CDE=∠DEB+∠B得45+22.5+x=2x+
,由∠CDE=∠DEB+∠B得45+22.5+x=2x+![]() ,此方程无解,所以DE=BE不成立
,此方程无解,所以DE=BE不成立
综上所述: ∠B=45![]() 或∠B=30
或∠B=30![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,点 A1、A2、A3、…在射线 ON 上,点 B1、B2、B3、…在射线 OM 上;△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形.若 OA1=1,则△A2015B2015A2016 的边长为 ( )
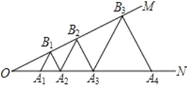
A. 4028 B. 4030 C. 22014 D. 22015
-
科目: 来源: 题型:
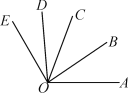
查看答案和解析>>【题目】如图,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOC=70°,∠COE=50°,那么∠BOD是多少度?
(2)如果∠BOD=70°,那么∠AOE是多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形 ABCD 中,AB⊥AD,BC⊥DC,点 M、N 分别是 AB、BC 边上的动点,∠B=56°.当△DMN 的周长最小时,则∠MDN 的度数是_____

-
科目: 来源: 题型:
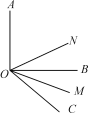
查看答案和解析>>【题目】(1)如图,∠AOB=90°,∠BOC=40°,ON平分∠AOC,OM平分∠BOC,求∠MON的度数;
(2)如果(1)中∠BOC=α,且α<90°,其他条件不变,求∠MON的度数;
(3)如果(1)中∠AOB=β,且β<90°,其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果中能得到什么规律?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1) [(x-y)2+(x+y)(x-y)]÷2x,其中 x=3,y=-2
(2)已知
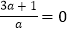 ,求
,求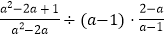 的值.
的值.
相关试题

