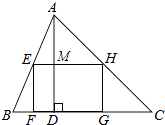
【题目】如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF= ![]() EH,那么EH的长为 .
EH,那么EH的长为 . 
参考答案:
【答案】![]()
【解析】解:如图所示:
∵四边形EFGH是矩形,
∴EH∥BC,
∴△AEH∽△ABC,
∵AM⊥EH,AD⊥BC,
∴ ![]() ,
,
设EH=3x,则有EF=2x,AM=AD﹣EF=2﹣2x,
∴ ![]() ,
,
解得:x= ![]() ,
,
则EH= ![]() .
.
故答案为: ![]() .
.
设EH=3x,表示出EF,由AD﹣EF表示出三角形AEH的边EH上的高,根据三角形AEH与三角形ABC相似,利用相似三角形对应边上的高之比等于相似比求出x的值,即为EH的长.此题考查了相似三角形的判定与性质,以及矩形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:cos60°﹣2﹣1+
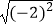 ﹣(π﹣3)0 .
﹣(π﹣3)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F, ∠1+∠2=90°.

(1)AB与CD平行吗?试说明理由.
(2)试探究∠2与∠3的数量关系.
-
科目: 来源: 题型:
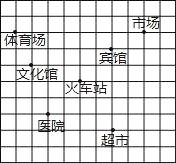
查看答案和解析>>【题目】如图,这是某市部分简图,为了确定各建筑物的位置:
(1)请你以火车站为原点建立平面直角坐标系.
(2)写出市场的坐标为 ;超市的坐标为 .
(3)请将体育场为A、宾馆为C和火车站为B看作三点用线段连起来,得△ABC,然后将此三角形向下平移4个单位长度,画出平移后的△A1B1C1,并求出其面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=
 AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,射线
,射线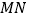 分别和直线
分别和直线 交于点
交于点 ,射线
,射线 分别和直线
分别和直线 交于点
交于点 ,点
,点 在射线
在射线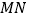 上运动(
上运动( 点与
点与 三点不重合),设
三点不重合),设 ,
, ,
, .
.
(1)如果点
 在
在 两点之间运动时,
两点之间运动时, 之间有何数量关系?请说明理由;
之间有何数量关系?请说明理由;(2)如果点
 在
在 两点之外运动时,
两点之外运动时, 之间有何数量关系?(只需写出结论,不必说明理由)
之间有何数量关系?(只需写出结论,不必说明理由) -
科目: 来源: 题型:
查看答案和解析>>【题目】若把不等式组
 的解集在数轴上表示出来,则其对应的图形为
的解集在数轴上表示出来,则其对应的图形为A. 长方形 B. 线段 C. 射线 D. 直线
相关试题

