【题目】如图,已知![]() ,射线
,射线![]() 分别和直线
分别和直线![]() 交于点
交于点![]() ,射线
,射线![]() 分别和直线
分别和直线![]() 交于点
交于点![]() ,点
,点![]() 在射线
在射线![]() 上运动(
上运动(![]() 点与
点与![]() 三点不重合),设
三点不重合),设![]() ,
,![]() ,
,![]() .
.

(1)如果点![]() 在
在![]() 两点之间运动时,
两点之间运动时,![]() 之间有何数量关系?请说明理由;
之间有何数量关系?请说明理由;
(2)如果点![]() 在
在![]() 两点之外运动时,
两点之外运动时,![]() 之间有何数量关系?(只需写出结论,不必说明理由)
之间有何数量关系?(只需写出结论,不必说明理由)
参考答案:
【答案】(1)γ=α+β(2)详见解析
【解析】分析:(1)过点P作P作PF∥l1因为l1//l2则l2//PF,根据两直线平行,内错角相等即可证明γ=α+β,(2) 过点P作P作PF∥l1因为l1//l2则l2//PF,根据两直线平行,内错角相等进行角度转化再根据三角形外角性质可证明∠β=∠γ+∠α,同理可得,当点P在AN上运动时,∠α=∠γ+∠β.
(1)证明:过点P作l3//l1,
∵l1//l2,
∴l2//l3,
∴γ=α+β.
(2)点P在射线AN上时:γ=α-β,
点P在射线BM上时:γ=β-α.
证明:过点P作l3//l1,
∵l1//l2,
∴l2//l3,
∴γ=α+β.
详解:(1)∠γ=α+∠β,
理由:过点P作PF∥l1(如图1),
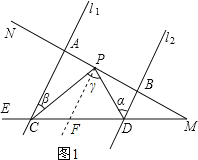
∵l1∥l2,
∴PF∥l2,
∴∠α=∠DPF,∠β=∠CPF,
∴∠γ=∠DPF+∠CPF=α+∠β,
(2)当点P在MB上运动时(如图2),

∵l1∥l2,
∴∠β=∠CFD,
∵∠CFD是△DFP的外角,
∴∠CFD=∠α+∠γ,
∴∠β=∠γ+∠α,
同理可得,当点P在AN上运动时,∠α=∠γ+∠β.
-
科目: 来源: 题型:
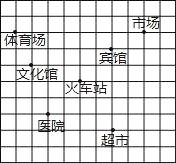
查看答案和解析>>【题目】如图,这是某市部分简图,为了确定各建筑物的位置:
(1)请你以火车站为原点建立平面直角坐标系.
(2)写出市场的坐标为 ;超市的坐标为 .
(3)请将体育场为A、宾馆为C和火车站为B看作三点用线段连起来,得△ABC,然后将此三角形向下平移4个单位长度,画出平移后的△A1B1C1,并求出其面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=
 EH,那么EH的长为 .
EH,那么EH的长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=
 AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF -
科目: 来源: 题型:
查看答案和解析>>【题目】若把不等式组
 的解集在数轴上表示出来,则其对应的图形为
的解集在数轴上表示出来,则其对应的图形为A. 长方形 B. 线段 C. 射线 D. 直线
-
科目: 来源: 题型:
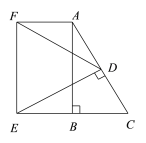
查看答案和解析>>【题目】Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,从D作DE⊥AC与CB的延长线交于点E,以AB、BE为邻边作矩形ABEF,连结DF,则DF的长是( )
A. 4
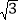 B. 3
B. 3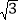 C. 2
C. 2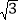 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

相关试题

