【题目】如图是小明用七巧板拼出的图案.
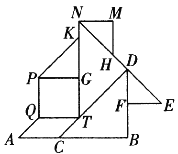
(1)请赋予该图形一个积极的含义;
(2)请你找出图中2组平行线段和2对互相垂直的线段,用符号表示它们;
(3)找出图中一个锐角、一个钝角和一个直角,将它们表示出来,并指出它们的度数.
参考答案:
【答案】(1)答案不唯一,如别墅; (2)答案不唯一,如:![]() ,
,![]() ,
,![]() ,
,![]() ; (3)答案不唯一,如锐角:
; (3)答案不唯一,如锐角:![]() ,度数为45°;直角:
,度数为45°;直角:![]() ,度数为90°;钝角:
,度数为90°;钝角: ![]() ,度数为135°.
,度数为135°.
【解析】
解答此题要熟悉七巧板的结构:五个等腰直角三角形(有两对全等三角形);一个正方形;一个平行四边形,根据这些图形的性质便可解答.
(1)别墅;
(2)PK∥AQ∥CD,MN∥PG∥EF∥QT∥AB,
PG⊥NT,DB⊥BC;
(3)锐角:∠KPG=45°,
直角:∠PQT=90°,
钝角:∠AQT=135°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①相等的角是对顶角;②若
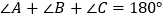 ,则
,则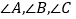 互补;③同一平面内的三条直线
互补;③同一平面内的三条直线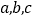 ,若
,若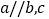 与
与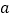 相交,则
相交,则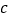 与
与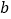 相交;④在同一平面内,两条不重合的直线的位置关系可能是平行或垂直;⑤有公共顶点并且相等的角是对顶角.其中正确的有( )
相交;④在同一平面内,两条不重合的直线的位置关系可能是平行或垂直;⑤有公共顶点并且相等的角是对顶角.其中正确的有( )A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.
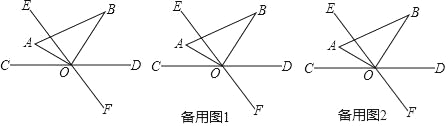
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】陈老师从拉面的制作中受到启发,设计了一个数学问题:如图,在数轴上截取从原点到1的对应点的线段
 ,对折后(点
,对折后(点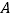 与
与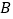 重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(如在第一次操作后,原线段
重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(如在第一次操作后,原线段 上的
上的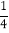 和
和 均变成
均变成 ,
, 变成1等).那么在线段
变成1等).那么在线段 上(除
上(除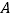 、
、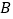 )的点中,在第
)的点中,在第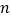 次操作后,恰好被拉到与1重合的点所对应的数为________________.
次操作后,恰好被拉到与1重合的点所对应的数为________________.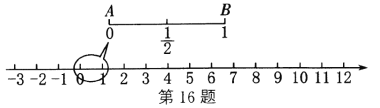
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是直线
是直线 上的一点,
上的一点, 是任意一条射线,
是任意一条射线, 平分
平分 ,
, 平分
平分 .
.(1)图中
 的补角为 ;
的补角为 ;(2)若
 ,求
,求 的度数;
的度数;(3)
 与
与 存在怎样的数量关系?
存在怎样的数量关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图①,若点O在边BC上,求证:AB=AC;
(2)如图②,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
我们知道:一条线段有两个端点,线段
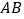 和线段
和线段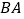 表示同一条线段. 若在直线
表示同一条线段. 若在直线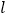 上取了三个不同的点,则以它们为端点的线段共有 条;若取了四个不同的点,则共有线段 条;…;依此类推,取了
上取了三个不同的点,则以它们为端点的线段共有 条;若取了四个不同的点,则共有线段 条;…;依此类推,取了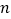 个不同的点,共有线段条.(用含
个不同的点,共有线段条.(用含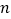 的代数式表示)
的代数式表示)类比探究:
以一个锐角的顶点为端点向这个角的内部引射线.
(1)若引出两条射线,则所得图形中共有 个锐角;
(2)若引出
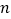 条射线,则所得图形中共有 个锐角.(用含
条射线,则所得图形中共有 个锐角.(用含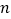 的代数式表示)
的代数式表示)拓展应用:
一条铁路上共有8个火车站,若一列火车往返过程中必须停靠每个车站,则铁路局需为这条线路准备多少种车票?
相关试题

