【题目】如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.
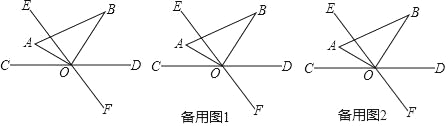
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
参考答案:
【答案】(1)60°;(2)若直线EF平分∠BOD,t的值为12s或36s.
【解析】试题分析:(1)根据角平分线的性质,可得∠AOC的值,再根据互为补角和互为余角的性质,求出∠BOD的值;
(2)①根据题意,分为OE平分∠AOB和OF平分∠AOB两种情况讨论求解;
②根据题意,分两种情况:当OE平分∠BOD和OF平分∠BOD时,进行画图求解.
试题解析:(1)∵∠COE=60°,OA平分∠COE,
∴∠AOC=30°,
又∵∠AOB=90°,
∴∠BOD=180°﹣30°﹣90°=60°;
(2)①分两种情况:
当OE平分∠AOB时,∠AOE=45°,
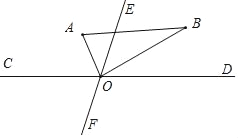
即9t+30°﹣3t=45°,
解得t=2.5;
当OF平分∠AOB时,AOF=45°,

即9t﹣150°﹣3t=45°,
解得t=32.5;
综上所述,当t=2.5s或32.5s时,直线EF平分∠AOB;
②t的值为12s或36s.
分两种情况:
当OE平分∠BOD时,∠BOE=![]() ∠BOD,
∠BOD,
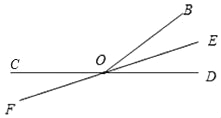
即9t﹣60°﹣3t=![]() (60°﹣3t),
(60°﹣3t),
解得t=12;
当OF平分∠BOD时,∠DOF=![]() ∠BOD,
∠BOD,
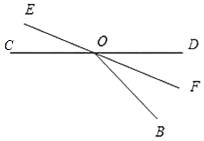
即3t﹣(9t﹣240°)=![]() (3t﹣60°),
(3t﹣60°),
解得t=36;
综上所述,若直线EF平分∠BOD,t的值为12s或36s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(3,3),B(5,3).
(1)在y轴的负方向上有一点C(如图),使得四边形AOCB的面积为18,求C点的坐标;
(2)将△ABO先向上平移2个单位,再向左平移4个单位,得△A1B1O1
①直接写出B1的坐标:B1( )
②求平移过程中线段OB扫过的面积.

-
科目: 来源: 题型:
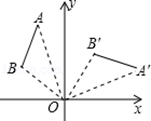
查看答案和解析>>【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某学校在“国学经典”中新建了一座吴玉章雕塑,小林站在距离雕塑3米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:
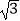 ≈1.7)
≈1.7)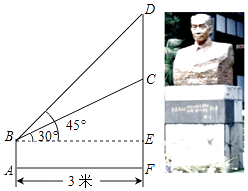
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年我县中考的体育测试成绩改为等级制,即把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格.我县5月份举行了全县九年级学生体育测试.现从中随机抽取了部分学生的体育成绩,并将其绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
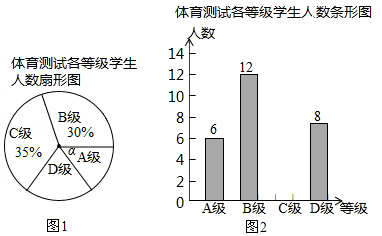
(1)本次抽样测试的学生人数是;
(2)图1中∠α的度数是 , 并把图2条形统计图补充完整;
(3)该县九年级有学生9000名,如果全部参加这次中考体育科目测试,请估算不及格的人数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的三个外角的度数比为 2:3:4,则它的最小内角的度数是( )
A.20°B.40°C.60°D.80°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线AB∥CD.
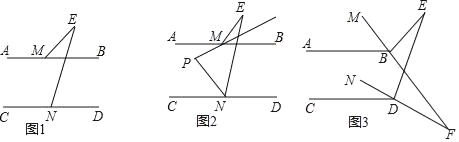
(1)如图1,直接写出∠BME、∠E、∠END的数量关系为 ;
(2)如图2,∠BME与∠CNE的角平分线所在的直线相交于点P,试探究∠P与∠E之间的数量关系,并证明你的结论;
(3)如图3,∠ABM=
 ∠MBE,∠CDN=
∠MBE,∠CDN= ∠NDE,直线MB、ND交于点F,则
∠NDE,直线MB、ND交于点F,则 = .
= .
相关试题

