【题目】在矩形ABCD中,已知两邻边AD=12,AB=5,P是AD边上异于A和D的任意一点,且PE⊥BD,PF⊥AC,E、F分别是垂足,那么PE+PF= . 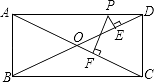
参考答案:
【答案】![]()
【解析】解:如图,过A作AG⊥BD于G, 则S△AOD= ![]() ×OD×AG,S△AOP+S△POD=
×OD×AG,S△AOP+S△POD= ![]() ×AO×PF+
×AO×PF+ ![]() ×DO×PE=
×DO×PE= ![]() ×DO×(PE+PF),
×DO×(PE+PF),
∵S△AOD=S△AOP+S△POD ,
∴PE+PF=AG,
∵AD=12,AB=5,
∴BD= ![]() =13,
=13,
∴ ![]() ,
,
∴ ![]() .
.
故答案为: ![]() .
.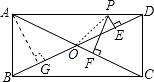
首先过A作AG⊥BD于G.根据等腰三角形底边上的任意一点到两腰距离的和等于腰上的高,则PE+PF=AG.利用勾股定理求得BD的长,再根据三角形的面积计算公式求得AG的长,即为PE+PF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
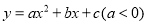 与双曲线
与双曲线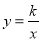 全相交于点A、B,且抛物线经过坐标原点,点
全相交于点A、B,且抛物线经过坐标原点,点 的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.
的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.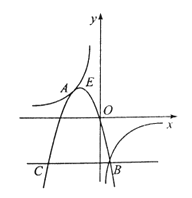
(1)求双曲线和抛物线的解析式;
(2)计算
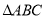 与
与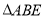 的面积;
的面积;(3)在抛物线上是否存在点D,使
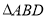 的面积等于
的面积等于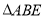 的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.
的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
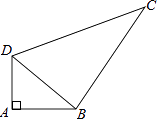
查看答案和解析>>【题目】如图,四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠A=90°,计算四边形ABCD的面积 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若要(a﹣1)a﹣4=1成立,则a=_____.
-
科目: 来源: 题型:
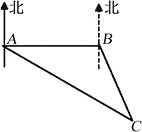
查看答案和解析>>【题目】如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:4﹣y2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E为平行四边形ABCD中DC边的延长线上一点,且CE=DC,连接AE分别交BC,BD于点F,G,连接BE.
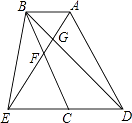
(1)求证:△AFB≌△EFG;
(2)判断CF与AD的关系,并说明理由.
相关试题

