【题目】端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进![]() 、
、![]() 两种粽子1100个,购买
两种粽子1100个,购买![]() 种粽子与购买
种粽子与购买![]() 种粽子的费用相同,已知
种粽子的费用相同,已知![]() 粽子的单价是
粽子的单价是![]() 种粽子单价的1.2倍.
种粽子单价的1.2倍.
(1)求![]() 、
、![]() 两种粽子的单价各是多少?
两种粽子的单价各是多少?
(2)若计划用不超过7000元的资金再次购买![]() 、
、![]() 两种粽子共2600个,已知
两种粽子共2600个,已知![]() 、
、![]() 两种粽子的进价不变,求
两种粽子的进价不变,求![]() 中粽子最多能购进多少个?
中粽子最多能购进多少个?
参考答案:
【答案】(l)![]() 种粽子的单价是3元,
种粽子的单价是3元,![]() 种粽子的单价是2.5元;(2)
种粽子的单价是2.5元;(2)![]() 种粽子最多能购进1000个.
种粽子最多能购进1000个.
【解析】
(1)根据题意列出分式方程计算即可,注意根的验证.
(2)根据题意列出不等式即可,根据不等式的性质求解.
(l)设![]() 种粽子的单价为
种粽子的单价为![]() 元,则
元,则![]() 种粽子的单价为
种粽子的单价为![]() 元
元
根据题意,得
![]()
解得:![]()
经检验,![]() 是原方程的根
是原方程的根
![]()
所以![]() 种粽子的单价是3元,
种粽子的单价是3元,![]() 种粽子的单价是2.5元
种粽子的单价是2.5元
(2)设![]() 种粽子购进
种粽子购进![]() 个,则购进
个,则购进![]() 种粽子
种粽子![]() 个
个
根据题意,得
![]()
解得![]()
所以,![]() 种粽子最多能购进1000个
种粽子最多能购进1000个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(-4,0)、B(0,2),点P(a,a).
(1)当a=2时,将△AOB绕点P(a,a)逆时针旋转90°得△DEF,点A的对应点为D,点O的对应点为E,点B的对应点为点F,在平面直角坐标系中画出△DEF,并写出点D的坐标 ;
(2)作线段AB关于P点的中心对称图形(点A、B的对应点分别是G、H),若四边形ABGH是正方形,则a= .
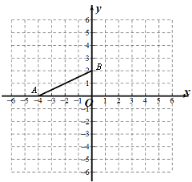
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校创新能力大赛的笔试情况,随机抽查了部分参赛同学的成绩,整理并制作了如下统计表和统计图(不完整) ,请根据图表中提供的信息解答问题:
得分
频数
百分比
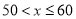
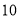
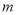
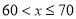

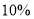
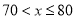
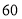
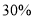
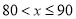
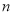
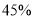
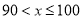

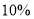

(1)本次调查的总人数为_______人;
(2)在统计表中,
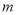 =____,
=____,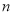 =__;在扇形统计图中“
=__;在扇形统计图中“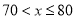 ”所在扇形的圆心角的度数为_______
”所在扇形的圆心角的度数为_______(3)补全频数分布直方图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】快递公司准备购买机器人来代替人工分拣已知购买- 台甲型机器人比购买-台乙型机器人多
 万元;购买
万元;购买 台甲型机器人和
台甲型机器人和 台乙型机器人共需
台乙型机器人共需 万元.
万元.(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型、乙型机器人每台每小时分拣快递分别是
 件、
件、 件,该公司计划最多用
件,该公司计划最多用 万元购买
万元购买 台这两种型号的机器人.该公司该如何购买,才能使得每小时的分拣量最大?
台这两种型号的机器人.该公司该如何购买,才能使得每小时的分拣量最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】现有6张正面分别标有数字﹣1,0,1,2,3,4的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,则使得关于x的二次函数y=x2﹣2x+a﹣2与x轴有交点,且关于x的分式方程
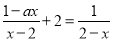 有解的概率为( )
有解的概率为( )A.
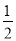 B.
B. 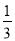 C.
C. 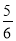 D.
D. 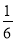
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac,
其中正确的有( )

A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
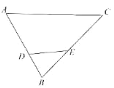
查看答案和解析>>【题目】尺规作图(不用写出作法,保留作图痕迹):
(1)在 DE 的上方,求作
 FDE,使得
FDE,使得 FDE≌
FDE≌ BDE;
BDE; (2)若∠B=50°,则∠ADF+∠CEF= °.
相关试题

