【题目】(1)请你根据下面画图要求,在图①中完成画图操作并填空.
如图①,△ABC中,∠BAC=30°,∠ACB=90°,∠PAM=∠A.
操作:(1)延长BC.
(2)将∠PAM绕点A逆时针方向旋转60°后,射线AM交BC的延长线于点D.
(3)过点D作DQ∥AB.
(4)∠PAM旋转后,射线AP交DQ于点G.
(5)连结BG.
结论:![]() = .
= .
(2)如图②,△ABC中,AB=AC=1,∠BAC=36°,进行如下操作:将△ABC绕点A按逆时针方向旋转α度角,并使各边长变为原来的n倍(n>1),得到△AB′C′.当点B、C、B′在同一条直线上,且四边形ABB′C′为平行四边形时(如图③),求a和n的值.

参考答案:
【答案】(1)![]() ;(2)72°;2.62.
;(2)72°;2.62.
【解析】
试题分析:(1)根据旋转得出△ABC~△AGD,设AB为2,根据30°的直角三角形的性质得出AD=2![]() ,进一步得出AG=4,可得
,进一步得出AG=4,可得![]() ;
;
(2)由四边形ABB′C′是平行四边形,易求得a=36°,又由△ABC∽△AB′C′,根据相似三角形的对应边成比例,继而求得答案.
试题解析:(1)如图:
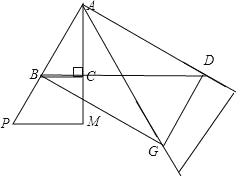
∵∠BAC=30°,∠ACB=90°,
∴∠PAM=∠A=30°,
∵∠PAM绕点A逆时针方向旋转60°,
∴∠BAG=60°,△ABC~△AGD,
∴∠GAD=∠BAC=∠MAG=30°,
∴△BAD是Rt△,∠ABD=60°,
∴∠ADB=30°,
设AB为2,则可得AD=![]() ,
,
∵DQ∥AB,∠BAD=90°
∴∠ADG=90°,
∵∠GAD=30°,AD=![]() ,
,
∴AG=4,
∴![]() ;
;
(2)∵四边形ABB′C′是平行四边形,
∴AC′∥BB′,
又∵∠BAC=36°,AB=AC
∴∠ABC=72°.
∴∠B′AC′=∠BAC=36°,
∴∠CAB′=36°,
∴α=180°-72°-36°=72°;
∴∠B′AC′=∠BAC=36°,而∠B=∠AB′C′,
∴△ABC∽△AB′C′,
∴AB:BB′=CB:AB,
∴AB2=CBAB′,
而 AB=1,
BC=2ABsin18°≈0.618,
所以可得n=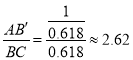 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:

(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=x2的图象向左、右平移后,得到的新图象的解析式不可能是( ).
A. y=(x+1)2 B. y=x2+4x+4 C. y=x2+4x+3 D. y=x2-4x+4
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣2x2y的系数为( )
A. 2 B. ﹣2 C. 3 D. ﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=
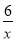 -1与函数y=kx交于点A(2,b)、B(-3,m)两点(点A在第一象限),
-1与函数y=kx交于点A(2,b)、B(-3,m)两点(点A在第一象限),(1)求b,m,k的值;
(2)函数y=
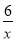 -1与x轴交于点C,求△ABC的面积.
-1与x轴交于点C,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】市政府建设一项水利工程,某运输公司承担运送总量为106m3的土石方任务,该公司有甲、乙两种型号的卡车共100辆,甲型车平均每天可以运送土石方80m3,乙型车平均每天可以运送土石方120m3,计划100天完成运输任务.
(1)该公司甲、乙两种型号的卡车各有多少台?
(2)如果该公司用原有的100辆卡车工作了40天后,由于工程进度的需要,剩下的所有运输任务必须在50天内完成,在甲型卡车数量不变情况下,公司至少应增加多少辆乙型卡车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=(m+1) x 2开口向上,则m的取值范围是___________.
相关试题

