【题目】操作:将一把三角尺放在如图①的正方形![]() 中,使它的直角顶点
中,使它的直角顶点![]() 在对角线
在对角线![]() 上滑动,直角的一边始终经过点
上滑动,直角的一边始终经过点![]() ,另一边与射线
,另一边与射线![]() 相交于点
相交于点![]() ,探究:
,探究:
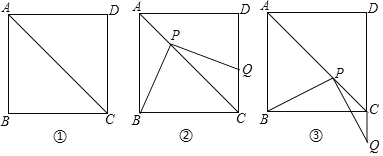
(1)如图②,当点![]() 在
在![]() 上时,求证:
上时,求证:![]() .
.
(2)如图③,当点![]() 在
在![]() 延长线上时,①中的结论还成立吗?简要说明理由.
延长线上时,①中的结论还成立吗?简要说明理由.
参考答案:
【答案】(1)证明见解析;(2)成立,理由见解析.
【解析】
(1)过点P作MN//BC,可以证明△PMQ≌△BNP,从而得出BP=QP;
(2)过点![]() 作
作![]() 于
于![]() ,
,![]() 交
交![]() 于点
于点![]() ,可以证明△PMQ≌△BNP,从而得出BP=QP;
,可以证明△PMQ≌△BNP,从而得出BP=QP;
(1)证明:过点![]() 作
作![]() ,分别交
,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,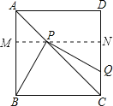
则四边形AMND和四边形BCNM都是矩形,△AMP和△CNP都是等腰直角三角形.
∴NP=NC=MB
∵∠BPQ=90°
∴∠QPN+∠BPM=90°,而∠BPM+∠PBM=90° ,
∴∠QPN=∠PBM,又∠QNP=∠PMB=90°,
在△QNP和△BMP中,
∠QNP=∠PMB,MB=NP,∠QPN=∠PBM
∴△QNP≌△PMB(ASA),
∴PQ=BP.
(2)成立.
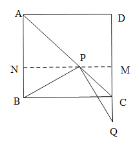
过点![]() 作
作![]() 于
于![]() ,
,![]() 交
交![]() 于点
于点![]()
在正方形![]() 中
中![]() ,
,![]()
∴![]()
∴![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,![]()
∴![]() ,
,
在![]() 和
和![]() 中,
中,
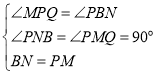 ,
,
∴![]() ,
,
∴![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AD∥BC,BC=4AD=4
 ,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于_____.
,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于_____.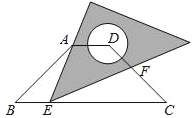
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图:


请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小张同学共调查了_____名居民的年龄,扇形统计图中a=_____;
(2)补全条形统计图,并注明人数;
(3)若在该辖区中随机抽取一人,那么这个人年龄是60岁及以上的概率为_____;
(4)若该辖区年龄在0~14岁的居民约有3500人,请估计该辖区居民人数是_____人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
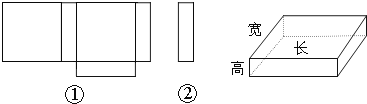
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在图上补 全.(请在备用图中画出所有可能)
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的4倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是720cm,求这个长方体纸盒的体积.
-
科目: 来源: 题型:
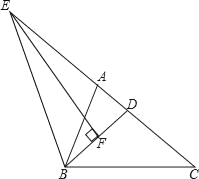
查看答案和解析>>【题目】在△ABC中,BD平分∠ABC,EF垂直平分BD交CA延长线于点E.
(1)求证:ED2=EAEC;
(2)若ED=6,BD=CD=3,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A、B两点之间的距离AB=|a-b|,线段AB的中点表示的数为
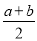

(问题情境)如图1,已知数轴上有三点
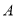 、
、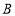 、
、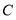 ,
,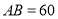 ,点
,点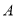 对应的数是
对应的数是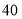 .
.(综合运用)(1)点B表示的数是__________.
(2)若
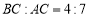 ,求点
,求点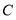 到原点的距离.
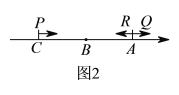
到原点的距离.(3)如图2,在(2)的条件下,动点
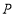 、
、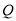 两点同时从
两点同时从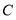 、
、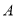 出发向右运动,同时动点
出发向右运动,同时动点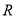 从点
从点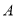 向左运动,已知点
向左运动,已知点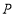 的速度是点
的速度是点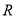 的速度的
的速度的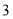 倍,点
倍,点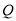 的速度是点
的速度是点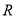 的速度
的速度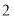 倍少
倍少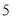 个单位长度/秒.经过
个单位长度/秒.经过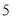 秒,点
秒,点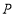 、
、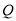 之间的距离与点
之间的距离与点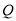 、
、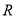 之间的距离相等,求动点
之间的距离相等,求动点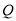 的速度;
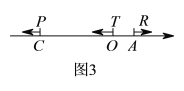
的速度;(4)如图3,在(2)的条件下,
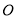 表示原点,动点
表示原点,动点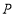 、
、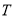 分别从
分别从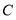 、
、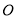 两点同时出发向左运动,同时动点
两点同时出发向左运动,同时动点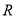 从点
从点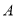 出发向右运动,点
出发向右运动,点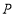 、
、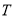 、
、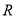 的速度分别为
的速度分别为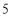 个单位长度/秒,
个单位长度/秒,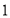 个单位长度/秒、
个单位长度/秒、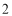 个单位长度/秒,在运动过程中,如果点
个单位长度/秒,在运动过程中,如果点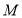 为线段
为线段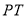 的中点,点
的中点,点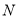 为线段
为线段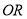 的中点.请问
的中点.请问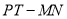 的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.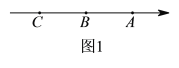
-
科目: 来源: 题型:
查看答案和解析>>【题目】为庆祝“春节”,市政府决定在市政广场上增一排灯花,其设计由以下图案逐步演变而成,其中圆圈代表灯花中的灯泡,n代表第n次演变过程,s代表第n次演变后的灯泡的个数,仔细观察下列演变过程,当n=7时,s=( ).
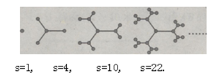
A.162B.176C.190D.214
相关试题

