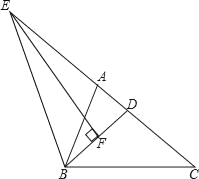
【题目】在△ABC中,BD平分∠ABC,EF垂直平分BD交CA延长线于点E.
(1)求证:ED2=EAEC;
(2)若ED=6,BD=CD=3,求BC的长.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】分析:(1)根据EF是BD的垂直平分线,可得EB=ED,再证明△EAB∽△EBC,列比例式为![]() ,将EB与ED替换可得结论;
,将EB与ED替换可得结论;
(2)根据△EAB∽△EBC,得![]() ,代入可得EA=4,作高线AG、DH,根据勾股定理求EF=
,代入可得EA=4,作高线AG、DH,根据勾股定理求EF=![]() ,利用面积法可得DH的长,再用平行相似得:△AGE∽△DHE,列比例式得AG的长,从而得EG的长,根据勾股定理得BC的长.
,利用面积法可得DH的长,再用平行相似得:△AGE∽△DHE,列比例式得AG的长,从而得EG的长,根据勾股定理得BC的长.
详解:(1)证明:∵EF是BD的垂直平分线,
∴EB=ED,
∴∠EDB=∠EBD,
∵∠EDB=∠C+∠DBC,∠EBD=∠ABE+∠ABD,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠C=∠ABE,
∵∠BEC=∠BEA,
∴△EAB∽△EBC,
∴![]() ,
,
∴EB2=EAEC,
∵EB=ED,
∴ED2=EAEC;
(2)∵ED=EB=6,BD=CD=3,
∴EC=6+3=9,
由(1)知:△EAB∽△EBC,
∴![]() ,
,
∴![]() ,EA=4,
,EA=4,
过A作AG⊥EB于G,过D作DH⊥EB于H,
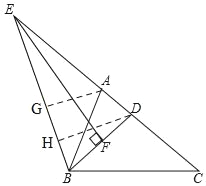
Rt△EFD中,ED=6,DF=![]() ,
,
∴EF=![]() ,
,
∴S△EBD=![]() EBDH=
EBDH=![]() BDEF,
BDEF,
∴DH=![]() EF=
EF=![]() ,
,
∵AG∥DH,
∴△AGE∽△DHE,
∴![]() ,
,
∴![]() ,
,![]() ,
,
由勾股定理得:EG=![]() ,
,
∴BG=6﹣![]() =
=![]() ,
,
由勾股定理得:AB=![]() ,
,
∵△EAB∽△EBC,
∴![]() ,
,
∴![]() ,
,
∴BC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD中,E、F分别在边AB、CD上,EF∥BC,AE:BE=1:2,对角线AC交EF于G,若BC=10cm,AD=6cm,则EF的长等于______ cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一水池有三个流量相同的注排两用水管,开一个水管一个小时注排水
 立方米.假设先开一个进水管注满半池水,再同时开三个进水管注满另一半池水;排水时,先用
立方米.假设先开一个进水管注满半池水,再同时开三个进水管注满另一半池水;排水时,先用 时间开三个水管同时排水,再用
时间开三个水管同时排水,再用 时间只开一个水管排水,把池中水排尽,这样排完一池水所花时间比前面注满一池水少用
时间只开一个水管排水,把池中水排尽,这样排完一池水所花时间比前面注满一池水少用 个小时,水池的容积是________立方米.
个小时,水池的容积是________立方米. -
科目: 来源: 题型:
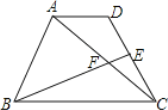
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,BC=2AD,点E是CD的中点,AC与BE交于点F,那么△ABF和△CEF的面积比是______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x,纵坐标y的对应值如表:
x
…
﹣2
﹣1
0
1
2
3
…
y
…
0
4
6
6
4
0
…
(1)求这个二次函数的表达式;
(2)直接写出当y<0时x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )

A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC,PF⊥CD,垂足分别为点E,F,连接AP,EF,给出下列四个结论:

①AP=EF;②∠PFE=∠BAP;③PD=
 EC;④△APD一定是等腰三角形.
EC;④△APD一定是等腰三角形.其中正确的结论有( ).
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

