搜索
【题目】如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（ ）
A.
B.2
C.
D.
参考答案：
【答案】B
【解析】解: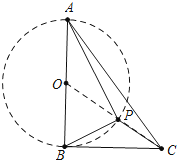
∵∠ABC=90°，
∴∠ABP+∠PBC=90°，
∵∠PAB=∠PBC，
∴∠BAP+∠ABP=90°，
∴∠APB=90°，
∴点P在以AB为直径的⊙O上，连接OC交⊙O于点P，此时PC最小，
在RT△BCO中，∵∠OBC=90°，BC=4，OB=3，
∴OC= 
=5，
∴PC=OC=OP=5﹣3=2．
∴PC最小值为2．
故选B．
【考点精析】本题主要考查了圆周角定理和点和圆的三种位置关系的相关知识点，需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；圆和点的位置关系：以点P与圆O的为例（设P是一点，则PO是点到圆心的距离），P在⊙O外，PO＞r；P在⊙O上，PO＝r；P在⊙O内，PO＜r才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】【操作发现】在计算器上输入一个正数，不断地按“
”键求算术平方根，运算结果越来越接近1或都等于1．
【提出问题】输入一个实数，不断地进行“乘以常数k，再加上常数b”的运算，有什么规律？
【分析问题】我们可用框图表示这种运算过程（如图a）．
也可用图象描述：如图1，在x轴上表示出x1 ， 先在直线y=kx+b上确定点（x1 ， y1），再在直线y=x上确定纵坐标为y1的点（x2 ， y1），然后再x轴上确定对应的数x2 ， …，以此类推．
【解决问题】研究输入实数x1时，随着运算次数n的不断增加，运算结果x，怎样变化．
（1）若k=2，b=﹣4，得到什么结论？可以输入特殊的数如3，4，5进行观察研究；
（2）若k＞1，又得到什么结论？请说明理由；
（3）①若k=﹣
，b=2，已在x轴上表示出x1（如图2所示），请在x轴上表示x2 ， x3 ， x4 ， 并写出研究结论；
②若输入实数x1时，运算结果xn互不相等，且越来越接近常数m，直接写出k的取值范围及m的值（用含k，b的代数式表示） -
科目： 来源： 题型：
查看答案和解析>>【题目】有一列按一定顺序和规律排列的数：
第一个数是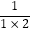
；
第二个数是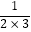
；
第三个数是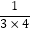
；
…
对任何正整数n，第n个数与第（n+1）个数的和等于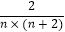
．
（1）经过探究，我们发现：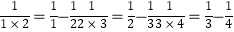
设这列数的第5个数为a，那么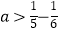
， 
， 
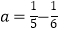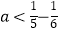，哪个正确？
请你直接写出正确的结论；
（2）请你观察第1个数、第2个数、第3个数，猜想这列数的第n个数（即用正整数n表示第n数），并且证明你的猜想满足“第n个数与第（n+1）个数的和等于 ”；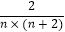
（3）设M表示
， 
， 
，…， 
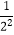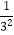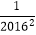，这2016个数的和，即 
，
求证：
． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知y是x的函数，自变量x的取值范围x＞0，下表是y与x的几组对应值：
x
…
1
2
3
5
7
9
…
y
…
1.98
3.95
2.63
1.58
1.13
0.88
…
小腾根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究．
下面是小腾的探究过程，请补充完整：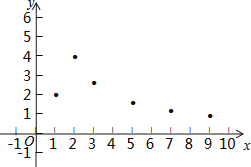
（1）如图，在平面直角坐标系xOy中，描出了以上表格中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
（2）根据画出的函数图象，写出：
①x=4对应的函数值y约为
②该函数的一条性质： -
科目： 来源： 题型：
查看答案和解析>>【题目】某中学为调查本校学生周末平均每天做作业所用时间的情况，随机调查了50名同学，下图是根据调查所得数据绘制的统计图的一部分．
请根据以上信息，解答下列问题：
（1）在这次调查的数据中，做作业所用时间的众数是 ，中位数是 ，平均数是 ；
（2）若该校共有2000名学生，根据以上调查结果估计该校全体学生每天做作业时间在3小时内（含3小时）的同学共有多少人?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最大值与最小值的和是（ ）
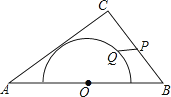
A.6
B.2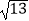
+1
C.9
D.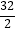
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将边长为10的正三角形OAB放置于平面直角坐标系xOy中，C是AB边上的动点（不与端点A，B重合），作CD⊥OB于点D，若点C，D都在双曲线y=
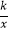上（k＞0，x＞0），则k的值为（ ）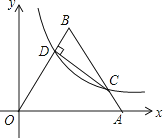
A.25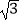
B.18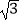
C.9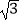
D.9
相关试题
