【题目】如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
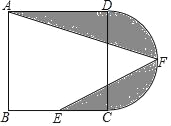
A. 18+36π B. 24+18π C. 18+18π D. 12+18π
参考答案:
【答案】C
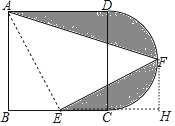
【解析】作FH⊥BC于H,连接FH,如图,根据正方形的性质和切线的性质得BE=CE=CH=FH=6,则利用勾股定理可计算出AE=6![]() ,通过Rt△ABE≌△EHF得∠AEF=90°,然后利用图中阴影部分的面积=S正方形ABCD+S半圆﹣S△ABE﹣S△AEF进行计算.
,通过Rt△ABE≌△EHF得∠AEF=90°,然后利用图中阴影部分的面积=S正方形ABCD+S半圆﹣S△ABE﹣S△AEF进行计算.
作FH⊥BC于H,连接FH,如图,
∵点E为BC的中点,点F为半圆的中点,
∴BE=CE=CH=FH=6,
AE=![]() =6
=6![]() ,
,
易得Rt△ABE≌△EHF,
∴∠AEB=∠EFH,
而∠EFH+∠FEH=90°,
∴∠AEB+∠FEH=90°,
∴∠AEF=90°,
∴图中阴影部分的面积=S正方形ABCD+S半圆﹣S△ABE﹣S△AEF
=12×12+![]() π62﹣
π62﹣![]() ×12×6﹣
×12×6﹣![]() 6
6![]() ×6
×6![]()
=18+18π.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
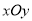 中,矩形
中,矩形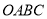 如图放置,动点
如图放置,动点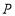 从
从 出发,沿所示方向运动,每当碰到矩形的边时反弹,每次反弹的路径与原路径成
出发,沿所示方向运动,每当碰到矩形的边时反弹,每次反弹的路径与原路径成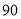 度角(反弹后仍在矩形内作直线运动),当点
度角(反弹后仍在矩形内作直线运动),当点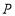 第
第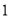 次碰到矩形的边时,点
次碰到矩形的边时,点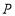 的坐标为
的坐标为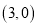 ;当点
;当点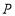 第
第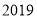 次碰到矩形的边时,点
次碰到矩形的边时,点 的坐标为 __________.
的坐标为 __________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点A(2,0)的两条直线
 ,
, 分别交
分别交 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB= .
.
(1)求点B的坐标;
(2)若△ABC的面积为4,求
 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,每个小方格的边长为一个单位长度.
(1)点
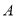 的坐标为 .点
的坐标为 .点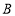 的坐标为 .
的坐标为 .(2)点
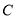 关于
关于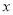 轴对称点的坐标为 ;
轴对称点的坐标为 ;(3)以
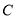 、
、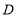 、
、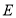 为顶点的三角形的面积为 ;
为顶点的三角形的面积为 ;(4)点
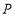 在
在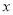 轴上,且
轴上,且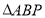 的面积等于
的面积等于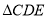 的面积,点
的面积,点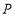 的坐标为 .
的坐标为 .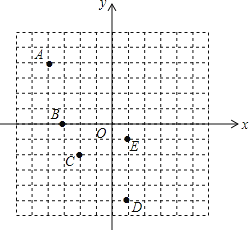
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平面直角坐标系xOy中,A(4,0)、B(0,3)、C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为( )
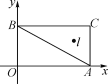
A. (-2,3) B. (-3,2) C. (3,-2) D. (2,-3)
-
科目: 来源: 题型:
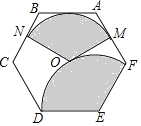
查看答案和解析>>【题目】如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.

相关试题

