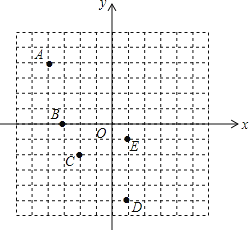
【题目】在平面直角坐标系中,每个小方格的边长为一个单位长度.
(1)点![]() 的坐标为 .点
的坐标为 .点![]() 的坐标为 .
的坐标为 .
(2)点![]() 关于
关于![]() 轴对称点的坐标为 ;
轴对称点的坐标为 ;
(3)以![]() 、
、![]() 、
、![]() 为顶点的三角形的面积为 ;
为顶点的三角形的面积为 ;
(4)点![]() 在
在![]() 轴上,且
轴上,且![]() 的面积等于
的面积等于![]() 的面积,点
的面积,点![]() 的坐标为 .
的坐标为 .
参考答案:
【答案】(1)![]() ;
;![]() ;(2)
;(2) ![]() ;(3)6 ;(4)
;(3)6 ;(4)![]() ;
;![]()
【解析】
(1)根据图形可得出点的坐标即可;
(2)根据关于x轴对称点的坐标特点:横坐标相等,纵坐标互为相反数,即可得出结果;
(3)以DE为底边,根据三角形的面积公式解答即可;
(4)以BP为底边,根据三角形的面积公式和x轴上坐标的特点解答即可.
解:(1)据图可得点A的坐标为(-4,4),点B的坐标为(-3,0),
故答案为:(-4,4)(-3,0);
(2)点C的坐标为(-2,-2,),可得点C关于x轴对称点的坐标为(-2,2);
故答案为:(-2,2);
(3)如图,作出△CDE,由图可知DE∥y轴,过点C作CH⊥DE于H,则根据点的坐标可知,DE=4,CH=3.
∴S△CDE=![]() ×4×3=6,
×4×3=6,
故答案为:6;
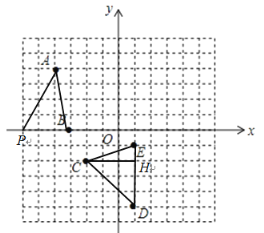
(4)因为△ABP的面积等于△CDE的面积=6,设点P的坐标为(x,0),则
6=![]() ×|x-(-3)|×4,解得x=0,或x=-6.
×|x-(-3)|×4,解得x=0,或x=-6.
∴点P坐标为:(-6,0)(0,0),
故答案为:(-6,0)(0,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从
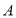 城出发匀速行驶至
城出发匀速行驶至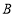 城.在整个行驶过程中,甲、乙两车离
城.在整个行驶过程中,甲、乙两车离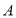 城的距离
城的距离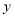 (千米)与甲车行驶的时间
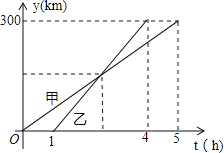
(千米)与甲车行驶的时间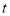 (小时)之间的函数关系如图所示.则下列结论:
(小时)之间的函数关系如图所示.则下列结论:①
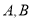 两城相距
两城相距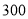 千米;
千米;②乙车比甲车晚出发
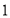 小时,却早到
小时,却早到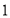 小时;
小时;③乙车出发后
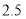 小时追上甲车;
小时追上甲车;④当甲、乙两车相距
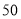 千米时,
千米时,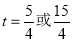
其中正确的结论有( )
A.
 个B.
个B.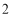 个C.
个C.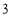 个D.
个D.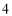 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
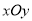 中,矩形
中,矩形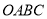 如图放置,动点
如图放置,动点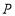 从
从 出发,沿所示方向运动,每当碰到矩形的边时反弹,每次反弹的路径与原路径成
出发,沿所示方向运动,每当碰到矩形的边时反弹,每次反弹的路径与原路径成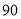 度角(反弹后仍在矩形内作直线运动),当点
度角(反弹后仍在矩形内作直线运动),当点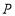 第
第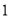 次碰到矩形的边时,点
次碰到矩形的边时,点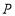 的坐标为
的坐标为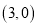 ;当点
;当点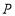 第
第 次碰到矩形的边时,点
次碰到矩形的边时,点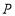 的坐标为 __________.
的坐标为 __________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点A(2,0)的两条直线
 ,
, 分别交
分别交 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB= .
.
(1)求点B的坐标;
(2)若△ABC的面积为4,求
 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
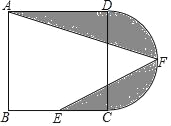
A. 18+36π B. 24+18π C. 18+18π D. 12+18π
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平面直角坐标系xOy中,A(4,0)、B(0,3)、C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为( )
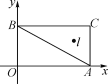
A. (-2,3) B. (-3,2) C. (3,-2) D. (2,-3)
-
科目: 来源: 题型:
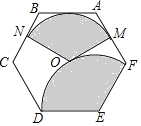
查看答案和解析>>【题目】如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=_____.
相关试题

