Question

【题目】在数学探究课上，老师出示了这样的探究问题，请你一起来探究：
已知：C是线段AB所在平面内任意一点，分别以AC，BC为边，在AB同侧作等边三角形ACE和BCD，联结AD，BE交于点P．
（1）如图1，当点C在线段AB上移动时，线段AD与BE的数量关系是： ．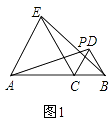

（2）如图2，当点C在直线AB外，且∠ACB＜120°，上面的结论是否还成立？若成立请证明，不成立说明理由．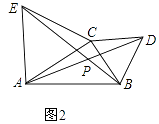

（3）在（2）的条件下，∠APE的大小是否随着∠ACB的大小的变化而发生变化，若变化，写出变化规律，若不变，请求出∠APE的度数．

Answer 1

【答案】
（1）解：AD=BE
（2）解：AD=BE成立．
证明：∵△ACE和△BCD是等边三角形
∴EC=AC，BC=DC，
∠ACE=∠BCD=60°，
∴∠ACE+∠ACB=∠BCD+∠ACB，即∠ECB=∠ACD；
在△ECB和△ACD中，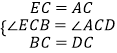
，
∴△ECB≌△ACD（SAS），
∴BE=AD
（3）解：∠APE不随着∠ACB的大小发生变化，始终是60°．
如图2，设BE与AC交于Q，
由（2）可知△ECB≌△ACD，
∴∠BEC=∠DAC
又∵∠AQP=∠EQC，∠AQP+∠QAP+∠APQ=∠EQC+∠CEQ+∠ECQ=180°
∴∠APQ=∠ECQ=60°，即∠APE=60°．
【解析】（1）∵△ACE、△CBD均为等边三角形，
∴AC=EC，CD=CB，∠ACE=∠BCD，
∴∠ACD=∠ECB；
在△ACD与△ECB中，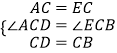
，
∴△ACD≌△ECB（SAS），
∴AD=BE，
所以答案是AD=BE．