【题目】如图,小强在河的一边,要测河面的一只船B与对岸码头A的距离,他的做法如下:
①在岸边确定一点C,使C与A,B在同一直线上;
②在AC的垂直方向画线段CD,取其中点O;
③画DF⊥CD使F、O、A在同一直线上;
④在线段DF上找一点E,使E与O、B共线.
他说测出线段EF的长就是船B与码头A的距离.他这样做有道理吗?为什么?
参考答案:
【答案】解:有道理,
∵DF⊥CD,AC⊥CD,
∴∠C=∠D=90°,
∵O为CD中点,
∴CO=DO,
在△ACO和△FDO中  ,
,
∴△ACO≌△FDO(ASA),
∴AO=FO,∠A=∠F,
在△ABO和△EOF中 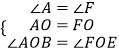 ,
,
∴△ABO≌△FEO(ASA),
∴EF=AB.
【解析】由作法,可运用二次全等法,构造出两对全等三角形ACO≌△FDO与△ABO≌△FEO,第一次全等为第二次全等准备条件AO=FO,∠A=∠F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P为∠AOB内一点,分别作出点P关于OA、OB的对称点P1、P2 , 连接P1P2交OA于M,交OB于N,若P1P2=6,则△PMN的周长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学探究课上,老师出示了这样的探究问题,请你一起来探究:
已知:C是线段AB所在平面内任意一点,分别以AC,BC为边,在AB同侧作等边三角形ACE和BCD,联结AD,BE交于点P.
(1)如图1,当点C在线段AB上移动时,线段AD与BE的数量关系是: .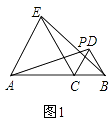
(2)如图2,当点C在直线AB外,且∠ACB<120°,上面的结论是否还成立?若成立请证明,不成立说明理由.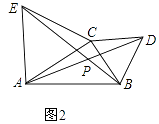
(3)在(2)的条件下,∠APE的大小是否随着∠ACB的大小的变化而发生变化,若变化,写出变化规律,若不变,请求出∠APE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算x7÷x4的结果等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一项工程,甲乙两公司合作,12天可以完成,如果甲乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,求甲乙两公司单独完成这项工程,各需多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知非等腰三角形的两边长分别是2 cm和9 cm,如果第三边的长为整数,那么第三边的长为( )
A. 8 cm或10 cm B. 8 cm或9 cm C. 8 cm D. 10 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD.求证:DB=DE.

相关试题

