搜索
【题目】给出下列算式
(1)观察上面一系列式子，猜想第五个式子？
(2)用含n的式子表示其规律(n为正整数)
(3)计算
的值，此时n是多少？
参考答案：
【答案】（1）
（2）（2n＋1）2（2n1）2＝8n；（3）2019220172的值8072，此时n是1009．
【解析】
（1）根据等式的左边是两个连续奇数的平方差，右边是8的倍数，写出下一个式子；
（2）根据已知数据得出两连续奇数的平方差的规律即可；
（3）根据（2）中的规律，即可解答．
（1）第五个式子为：
（2）∵
…
∴设n（n≥1）表示自然数，用关于n的等式表示这个规律为：（2n＋1）2（2n1）2＝8n；
（3）2n＋1＝2019，
解得：n＝1009，
∴2019220172＝8×1009＝8072．
答：2019220172的值8072，此时n是1009．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一个长方形运动场被分隔成ABABC共5个区，A区是边长为a m的正方形，C区是4个边长为b m的小正方形组成的正方形．
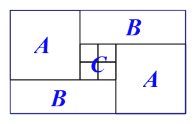
（1）列式表示每个B区长方形场地的周长，并将式子化简；
（2）列式表示整个长方形运动场的周长，并将式子化简；
（3）如果a＝40 m，b＝20 m，求整个长方形运动场的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算4×2.112－4×2.11×2.22＋2.222”，她觉得太麻烦，估计应该有可以简化计算的方法，就去请教崔老师．崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
（1）填写下表:
x＝－1，y＝1
x＝1，y＝0
x＝3，y＝2
x＝2，y＝－1
x＝2，y＝3
A＝2x－y
－3
2
4
5
1
B＝4x2－4xy＋y2
9
4
16
（2）观察表格，你发现A与B有什么关系?
解决问题:
（3）请利用A与B之间的关系计算:4×2.112－4×2.11×2.22＋2.222．
-
科目： 来源： 题型：
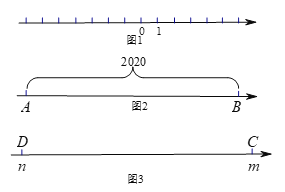
查看答案和解析>>【题目】已知在透明纸面上有一数轴(如图1)，折叠透明纸面．
（1）若表示1的点与表示－1的点重合，则表示－7的点与表示 的点重合；
（2）若表示－2的点与表示6的点重合，回答以下问题:
①表示12的点与表示 的点重合；
②如图2，若数轴上AB两点之间的距离为2020(点A在点B的左侧)，且AB两点经折叠后重合，则AB两点表示的数分别是 ．
（3）如图3，若m和n表示的点C和点D经折叠后重合(m＞n)，折痕与数轴的交点为折痕点．已知线段CD上两点P、Q (点P在点Q的左侧，PQ＜CD)，PQ＝a．当线段PQ的端点与折痕点重合时，求PQ两点表示的数分别是多少?(用含m，n，a的代数式表示)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题：探究一次函数y=kx+k+2（k是不为0常数）图象的共性特点，探究过程：小明尝试把x=-1代入时，发现可以消去k，竟然求出了y=2．老师问：结合一次函数图象，这说明了什么？小组讨论得出：无论k取何值，一次函数y=kx+k+2的图象一定经过定点（-1，2），老师：如果一次函数的图象是经过某一个定点的直线，那么我们把像这样的一次函数的图象定义为“点旋转直线”．已知一次函数y=（k+3）x+（k-1）的图象是“点旋转直线”
（1）一次函数y=（k+3）x+（k-1）的图象经过的定点P的坐标是__________．
（2）已知一次函数y=（k+3）x+（k-1）的图象与x轴、y轴分别相交于点A、B
①若△OBP的面积为3，求k值；
②若△AOB的面积为1，求k值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下表是小明记录的今年雨季一周河水的水位变化情况（上周末的水位达到警戒水位）．
星期
一
二
三
四
五
六
日
水位变化/米
+0.20
+0.81
﹣0.35
+0.03
+0.28
﹣0.36
﹣0.01
注：正号表示水位比前一天上升，负号表示水位比前一天下降．
（1）本周哪一天河流的水位最高？哪一天河流的水位最低？它们位于警戒水位之上还是之下？与警戒水位的距离分别是多少米？
（2）与上周相比，本周末河流水位是上升了还是下降了？
-
科目： 来源： 题型：
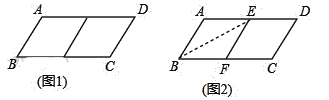
查看答案和解析>>【题目】邻边不相等的平行四边形纸片，剪去一个菱形，余下的一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；…依此类推，若第n次操作余下的四边形是菱形，则称原平行四边形为n阶准菱形，如图1，ABCD中，若AB=1，BC=2，则ABCD为1阶准菱形．
（1）猜想与计算：
邻边长分别为3和5的平行四边形是_______阶准菱形；已知ABCD的邻边长分别为a，b（a＞b），满足a=8b+r，b=5r，请写出ABCD___________阶准菱形．
（2）操作与推理：
小明为了剪去一个菱形，进行了如下操作：如图2，把ABCD沿BE折叠（点E在AD上），使点A落在BC边上的点F处，得到四边形ABFE．请证明四边形ABFE是菱形．
相关试题
