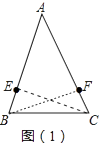
【题目】问题背景:如图(1),在△ABC中,已知AB=AC,BE=CF.
(1)发现问题:小华审题后发现,若连接CE,BF,则CE=BF,请说明理由;
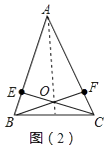
(2)提出问题:如图(2),设CE与BF交于点O,则直线AO是BC边的垂直平分线吗?试说明理由;
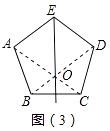
(3)解决问题:在图(3)中,是各边相等,各内角也相等的正五边形ABCDE,请你只用无刻度的直尺画出图中BC边的垂直平分线.
参考答案:
【答案】
(1)解:如图1中,连接EC、BF.
∵AB=AC,
∴∠ABC=∠ACB,
在△EBC和△FCB中,
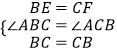 ,
,
∴△EBC≌△FCB,
∴CE=BF;
(2)解:结论:AO是BC边的中垂线,
理由:∵△EBC≌△FCB,
∴∠OEB=∠OFC,
在△EOB和△FOC中,
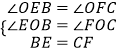 ,
,
∴△EOB≌△FOC,
∴OB=OC,又AB=AC,
∴AO是BC边的中垂线
(3)解:如图(3):连接AC、BD交于点O,作直线EO,直线EO即为线段BC的垂直平分线.
【解析】(1)首先依据等腰三角形的性质得到∠ABC=∠ACB,然后再依据SAS证明△EBC≌△FCB即可;
(2)证明△EOB≌△FOC,得到OB=OC,根据线段垂直平分线的判定定理得到答案;
(3)根据点到线段的两个端点的距离相等的点在线段的垂直平分线上作图即可.
【考点精析】关于本题考查的等腰三角形的性质,需要了解等腰三角形的两个底角相等(简称:等边对等角)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A,B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午2时骑摩托车按同路从A地出发驶往B地,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午行驶的时间t之间的关系.根据图象回答下列问题:
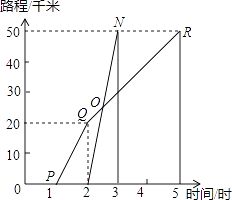
(1)甲在该日下午2﹣5时骑自行车的速度是多少?
(2)乙从出发大约用多长时间就能追上甲?
(3)甲骑自行车和乙骑摩托车在全程的平均速度分别是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】一种病毒的长度约为0.000072mm,用科学记数法表示0.000072为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣3[b﹣(3a2﹣3ab)]﹣[b+2(4a2﹣4ab)]
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A. -2是-4的平方根 B. 2是(-2)2的算术平方根
C. (-2)2的平方根是±2 D. 8的立方根是2
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程或方程组:
(1)x﹣4=3
(2)﹣(x﹣3)=3(2﹣5x)
(3)
(4) .
. -
科目: 来源: 题型:
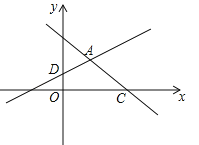
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=﹣x+3与x轴交于点C,与直线AD交于点A(
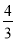 ,
,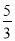 ),点D的坐标为(0,1)
),点D的坐标为(0,1)(1)求直线AD的解析式;
(2)直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.
相关试题

