【题目】如图所示,A,B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午2时骑摩托车按同路从A地出发驶往B地,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午行驶的时间t之间的关系.根据图象回答下列问题: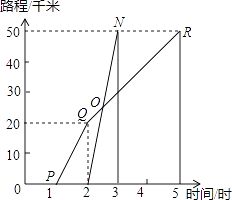
(1)甲在该日下午2﹣5时骑自行车的速度是多少?
(2)乙从出发大约用多长时间就能追上甲?
(3)甲骑自行车和乙骑摩托车在全程的平均速度分别是多少?
参考答案:
【答案】
(1)解:甲在该日下午2﹣5时骑自行车的速度是 ![]() =10千米/小时
=10千米/小时
(2)解:由图可知:M(2,0),N(3,50),Q(2,20),R(5,50)
设直线QR的函数表达式为y1=k1x+b1,
将Q(2,20),R(5,50)代入得:
![]() ,
,
解得 ![]() ,
,
设直线MN的函数表达式为y2=k2x+b2,
将M(2,0),N(3,50)代入得:
![]() ,
,
解得 ![]() ,
,
则y1=10x,y2=50x﹣100,
联立两式可得直线QR、MN的交点的坐标为(2.5,25).
所以乙出发半小时后追上甲
(3)解:乙的平均速度为 ![]() =50千米/时,甲的平均速度为
=50千米/时,甲的平均速度为 ![]() =12.5千米/时
=12.5千米/时
【解析】(1)根据速度=路程÷时间即可解决问题;
(2)先求得两函数的解析式,然后再组成方程组,求得两个函数交点的坐标即可;
(3)用各自的总路程÷各自的总时间,列式计算即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数﹣22 , (﹣2)3 , ﹣|﹣2|,
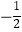 按从小到大的顺序排列为( )
按从小到大的顺序排列为( )
A.(﹣2)3<﹣22<﹣|﹣2|<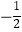
B.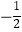 <﹣|﹣2|<﹣22<(﹣2)3
<﹣|﹣2|<﹣22<(﹣2)3
C.﹣|﹣2|<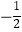 <﹣22<(﹣2)3
<﹣22<(﹣2)3
D.﹣22<(﹣2)3<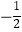 <﹣|﹣2|
<﹣|﹣2| -
科目: 来源: 题型:
查看答案和解析>>【题目】某绿色食品有限公司准备购进A和B两种蔬菜,B种蔬菜每吨的进价比A中蔬菜每吨的进价多0.5万元,经计算用4.5万元购进的A种蔬菜的吨数与用6万元购进的B种蔬菜的吨数相同,请解答下列问题:
(1)求A,B两种蔬菜每吨的进价;
(2)该公司计划用14万元同时购进A,B两种蔬菜,若A种蔬菜以每吨2万元的价格出售,B种蔬菜以每吨3万元的价格出售,且全部售出,请求出所获利润W(万元)与购买A种蔬菜的资金a(万元)之间的函数关系式;
(3)在(2)的条件下,要求A种蔬菜的吨数不低于B种蔬菜的吨数,若公司欲将(2)中的最大利润全部用于购买甲、乙两种型号的电脑赠给某中学,甲种电脑每台2100元,乙种电脑每台2700元,请直接写出有几种购买电脑的方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
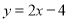 的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为
的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为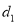 、
、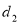 .
.(1)当P为线段AB的中点时,求
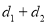 的值;
的值;(2)直接写出
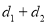 的范围,并求当
的范围,并求当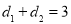 时点P的坐标;
时点P的坐标;(3)若在线段AB上存在无数个P点,使
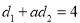 (a为常数),求a的值.
(a为常数),求a的值.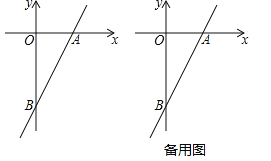
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种病毒的长度约为0.000072mm,用科学记数法表示0.000072为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣3[b﹣(3a2﹣3ab)]﹣[b+2(4a2﹣4ab)]
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:如图(1),在△ABC中,已知AB=AC,BE=CF.

(1)发现问题:小华审题后发现,若连接CE,BF,则CE=BF,请说明理由;
(2)提出问题:如图(2),设CE与BF交于点O,则直线AO是BC边的垂直平分线吗?试说明理由;
(3)解决问题:在图(3)中,是各边相等,各内角也相等的正五边形ABCDE,请你只用无刻度的直尺画出图中BC边的垂直平分线.
相关试题

