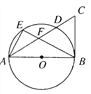
【题目】如图所示,AB是00的直径,BC是⊙O的切线,连接AC,交⊙0于D,E为弧AD上一点,连接AE,BE交AC于点F且![]() ,(1)求证CB=CF;(2)若点E到弦AD的距离为3,cos C=
,(1)求证CB=CF;(2)若点E到弦AD的距离为3,cos C=![]() ,求⊙O的半径.
,求⊙O的半径.
参考答案:
【答案】(1)证明见解析;(2)6
【解析】试题分析:(1)如图1,通过相似三角形![]() 的对应角相等推知,
的对应角相等推知,![]() 又由弦切角定理、对顶角相等证得
又由弦切角定理、对顶角相等证得![]() 最后根据等角对等边证得结论;
最后根据等角对等边证得结论;
(2)如图2,连接OE交AC于点G,设![]() 的半径是r.根据(1)中的相似三角形的性质证得∠4=∠5,所以由“圆周角、弧、弦间的关系”推知点E是弧
的半径是r.根据(1)中的相似三角形的性质证得∠4=∠5,所以由“圆周角、弧、弦间的关系”推知点E是弧![]() 的中点,则
的中点,则![]() 然后通过解直角
然后通过解直角![]() 求得
求得![]() ,则以求
,则以求![]() 的值.
的值.
试题解析:(1)证明:如图1,
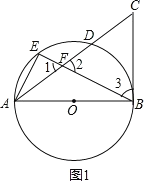
∵![]()
又∵∠AEF=∠AEB,
∴△AEF∽△AEB,
∴∠1=∠EAB.
∵∠1=∠2,∠3=∠EAB,
∴∠2=∠3,
∴CB=CF;
(2)如图2,连接OE交AC于点G,设![]() 的半径是r.
的半径是r.
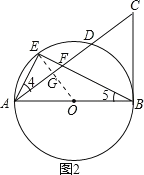
由(1)知,△AEF∽△AEB,则∠4=∠5.
∴.![]() =
=![]() ,
,
∴OE⊥AD,
∴EG=3
![]() 且
且![]()
![]()
![]() 即
即![]()
解得,r=6,即![]() 的半径是6.
的半径是6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的
 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这
 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师给学生出了一道题:
求(2a+b)(2a﹣b)+2(2a﹣b)2+(2ab2﹣16a2b)÷(﹣2a)的值,其中a=
 ,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”
,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”(1)你认为他们谁说的有道理?为什么?
(2)若xm等于本題计算的结果,试求x2m的值.
-
科目: 来源: 题型:
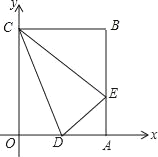
查看答案和解析>>【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:

设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】乐乐家附近的商场为了吸引顾客,设立了一个可以自由转动的转盘,AB为转盘直径,如图所示,并规定:顾客消费50元(含50元)以上,就能获得一次转盘的机会,如果转盘停止后,指针正好对准9折、8折、7折区域,顾客就可以获得相应的优惠
(1)某顾客消费40元,是否可以获得转盘的机会?
(2)某顾客正好消费66元,他转一次转盘,获得三种打折优惠的概率分别是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】小王周末骑电动车从家里出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离(米)与时间(分钟)之间的关系示意图,请根据图中提供的信息回答下列问题:
(1)在此变化过程中,自变量是 ,因变量是 .
(2)小王在新华书店停留了多长时间?
(3)买到书后,小王从新华书店到商场的骑车速度是多少?

相关试题

