【题目】我校在开展“三·五”奉献活动中,准备向镇敬老院捐赠一批帽子,已知买男式帽子用了180元,女式帽子的单价比男式帽子单价多2元.
(1)若原计划募捐380元,购买两种帽子共20顶,那么男、女式帽子的单价各是多少元?
(2)在这次捐款活动中,由于学生捐款踊跃,实际捐款566元,如果至少购买两种帽子共30顶,那么女式帽子最多能买几顶?
参考答案:
【答案】(1)男式帽子为18元/顶,女式为20元/顶;(2)女式帽子最多能购买12顶.
【解析】解:(1)设男式帽子为x元/顶,则女式帽子为(x+2)天/顶
![]()
去分母得,x2-17x-18=0
解得,x1=18,x2=-1(舍去)
经检验 x=18是原方程的根:
x+2=18+2=20(元)
因此,男式帽子为18元/顶,女式为20元/顶.
(2)设女式最多能买y顶
20y+(30-y)×18≤566
解得,y≤12
因此,女式帽子最多能购买12顶.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:(a+2)2+|b﹣3|=0,则(a+b)2009= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简下式,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中a=﹣2,b=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明过程:
已知:如图,∠D=123°,∠EFD=57°,∠1=∠2
求证:∠3=∠B
证明:∵∠D=123°,∠EFD=57°(已知)
∴∠D+∠EFD=180°
∴AD∥()
又∵∠1=∠2(已知)
∴∥BC(内错角相等,两直线平行)
∴EF∥()
∴∠3=∠B(两直线平行,同位角相等)
-
科目: 来源: 题型:
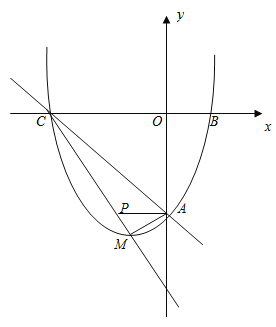
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c与x轴交于点B,C,与直线AC:y=-x-6交y轴于点A,点M是抛物线的顶点,且横坐标为-2.
(1)求出抛物线的表达式.
(2)判断△ACM的形状并说明理由.
(3)直线CM交y轴于点F,在直线CM上是否存在一点P,使∠CMA=∠PAF,若存在,求出P的坐标,若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】雾霾天气严重影响市民的生活质量,因此,空气质量备受人们关注,甲城某空气质量监测站点检测了该区域每天的空气质量情况,统计了2015年2月—5月份若干天的情况,并制订了如下两幅不完整的统计图,请根据图中信息,解答下列问题:


(1)统计图共统计了________天空气质量的情况.
(2)请将图中所缺部分补充完整,并计算空气质量为优的所在扇形的圆心角的度数?
(3)计算轻度污染的所占比例,并以此估计2016年2—5月份中大约有多少天受轻度污染?(最后结果用收尾法)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:aa3﹣(2a2)2+4a4
相关试题

